sums will set you free

how to teach your child numbers arithmetic mathematics

fractions, decimals, percentages and ratios 1

fractions, probability, percentage and proportion

Say one in a hundred fish are blue, this can be expressed and written numerically in several manners.

• Blue fish are a 1/100 fraction of a group of fish.
• The probability that a fish is blue is 1:100 (also called the ratio).
• The percentage of blue fish is 1%.
• The proportion of blue fish to other colours is one in a hundred.

fractions, decimals, percentages and ratios
are all effectively the ‘same’ thing   

Each of these are particular types of division sum (see the sub-sections of fractions). It is important to internalise this realisation right from the start. That is why here, all three topics are included on the same page. Once you understand one of these topics, you are in a position to understand them all. They are just different ways communicating and writing the same type of information.

All these descriptions are expressions of the same situation - one blue fish and ninety-nine other fish.

What we will do on this, and on other teaching sums pages, is show various methods of doing the same sort of sum, so that the learner will start to understand what is involved with each sort of sum; rather than just learning rules by heart.

Teaching in parrot lockstep, with rigid rules, does the opposite from showing a learner how to understand different situations. It may let learners go through doing sums like a parrot and achieve ‘the right answer’, but the long-term result is that the learners:

• do not understand what is going on,
• they cannot move flexibly around mathematics in the manner of holding a conversation in English - understanding the words and with a natural comprehension of the meanings,
• they do not know what the answers they have mean, or even where the answers come from in the real world,
• and they are unable to apply the mathematical tools to other situations.

I am going to start with fractions because they are probably the easiest method of expression/writing/form to understand.

I shall be giving you basic methods, and ways to illustrate and explain to a learner. There is no possible way a young person will fully grasp this after one example nor gain comfortable familiarity in a single day, so you will need to invent various versions (including repeats) of the sums until the pupil understands and remembers the methods fluently.

Cut a cake into four parts.

(See also and now for something completely different - a piece of cake)

Each part of the cake is described as one quarter [¼], or one fourth. One divided into four can be written as 1 divided by 4 [1 ÷ 4], another way is saying one divided by four, or ‘four into one’, or one divided into four parts.

As with any language usage, there is more than one way of saying or describing any situation. In schools in the Far East, each quarter would be taught as ‘one part of four’, and so on for other fractions.

The cat sat on the mat, or

the mat was under the sitting cat, or

the mat was on the floor and the cat was sitting on it.

It is useful and necessary for the learner to understand what the words mean in the real world, and so to extend their vocabulary and their language. Remember learning mathematics is really just learning more English. It is not some special or different subject. It is no different from learning about cats and mats.

Bad teaching or no teaching are by far the most widespread causes of poor learning. In mathematics, we can count cats or divide them into quarters (another thing which you should not try at home); or we may count and divide blocks or cakes.

Now back to the cake divided into four. Notice that we started by calling it one cake and now we have four quarters of one cake, or block.

If each of the quarters is then divided into four, so there are four quarters of each quarter, then the original whole cake, or block, will now be divided into sixteen parts.

In the written fraction ¼, the one above the line shows how many parts are included in the fraction (of the cake or block or anything you choose) - in this case one part, while the number below the line shows or indicates how many parts the complete object (cake, or anything) is divided.

Remember, the equals sign is a sort of balance point in an equation (sum)

site map

advertising disclaimer

See that if you add quarter of a cake to quarter of a cake, ¼ + ¼, you now have two quarters 2/4, or half a cake. Obviously, that is written as one over two, ½ , this can be described as one cake divided into two. If you add a quarter to a quarter to a quarter to a quarter, ¼ + ¼ + ¼ + ¼, you now have the whole cake, that is one cake, which can be written as 4/4, while three quarters of the cake will be written as ¾.

As you will notice, the four quarters of the cake, 4/4 [2], which as already said means four divided by four, and we know very well that four divided by four is one - that is in this case, one cake.

Now it is important for an understanding of fractions, that at each stage the numbers are attached clearly to the physical objects and the manipulation of those physical objects. As we build this connection, it will later mean that as the learner moves to calculating with the numbers, they will acquire a feel for whether the sums make sense. The learner will be able to return to cakes and blocks, if confused, in order to make sure that the sums work in the real world.

We have two quarters 2/4, which we then said is half a cake ½, and simply, by looking at the cake or the blocks, you can immediately see with your eyesy-piesyes that two quarters of the cake is indeed half the cake. Thus it is clear that half is the ‘same’ as (equal to) two quarters: 1/2=2/4.

If you look closely, you will see that, in the expression 2/4, if we divide the two by two, the result is one; and if we divide the four by two, the result is two. That is by carrying out this rule - do the same to the top and to the bottom - the result works in this case. Soon we shall move on to see whether this magical performance will continue to work in all other circumstances.

If we go up the leaning Tower of Pisa and drop stones, we will see that the stones usually fall to the ground, maybe sometimes bouncing of the heads of passers by. Of course, you can try this while sitting on a chair, when you may bean a mouse. That these objects fall when you let go of them, eventually becomes so obvious and happens with such predictability, that you decide that this phenomenon is a rule in the real world. If you drop a computer, or an elephant, or even yourself, each will fall. So, when you pick yourself up, be careful not to drop yourself.

In due course, you will probably be prepared to agree that when you divide (or multiply) the top and bottom parts of a division sum, or fraction, by the same number, the value after these divisions or multiplications (the value being the amount of cake) does not vary from the fraction before the division or multiplication. 50/100, 6/12, 4/8, 3/6, 2/4, 1/2 are all equivalent fractions and all indicate one half.

adding or subtracting fractions

simple fractions

Some examples of simple additions with fractions:

three quarters plus one quarter equals four quarters, which equals one
3/4 + 1/4 = 4/4 = 1

one third plus two thirds equals three thirds, which equals one
1/3 + 2/3 = 3/3 = 1

Some examples of simple subtractions with fractions:

one minus one third equals two thirds: 1- 1/3 = 2/3

one minus three quarters equals one quarter : 1 - 3/4 = 1/4

Note that with these simple sums, the number underneath - the divisor or denominator - is the same for all parts of the sum. Each fraction being added the same sort of fraction, for instance: quarters, or tenths, or eighteenths.

Simple multiplications and divisions with fractions are on the next page - fractions, decimals, percentages and ratios 2. That deals with more complicated fraction sums.

fractions including whole numbers

These are fractions such as one and a quarter: 1 1/4.
Adding such fractions is found in sums such as
1 1/4 + 1 1/4, or 2 1/5 + 3 2/5.

When adding such fractions together, you add the whole numbers together and add the fractions together:
1 + 1 + 1/4 + 1/4.

Thus, 1 1/4 + 1 1/4

= 2 + (1/4 + 1/4)
= 2 + 2/4
= 2 2/4 = 2 1/2

 

Or, 2 1/5 +3 2/5

= 5 + (1/5 + 2/5)
= 5 +3/5
= 5 3/5

 

And with three fractions including whole numbers:
1 5/6 + 1 1/6 + 1 2/6

= 3 + (5/6 + 1/6 + 2/6)
= 3 + 8/6

Oh wow, you say, 8/6 is more than 6/6 (or one)!
Yes, so split 8/6 into a whole number and a fraction by subtracting 6/6 (that is, 1) from 8/6:
8/6 - 6/6 = 2/6.

To recap, 1 5/6 + 1 1/6 + 1 2/6

= 3 + 1 +2/6
= 4 2/6
= 4 1/3.

 

Another way of going about this last sum is to turn everything into sixths [1/6s] .
So ... for 1 5/6, 1 is equivalent to 6/6, that is six parts of something divided into six. Now to that add the 5/6. First, remember that 5/6 is five parts of something divided into six . So 6/6 [six parts of six parts] plus 5/6 [five parts of six parts] makes 11/6.
Now 1 1/6 is 6/6 plus 1/6, which makes 7/6,
while 1 2/6 is 6/6 plus 2/6, which makes 8/6.
Thus, we add 11/6 + 7/6 + 8/6, which makes 26/6. Now this is 26 parts of something divided into six. So let’s divide 26 by 6, and the result is 4 2/6.
The final sum is 1 5/6 + 1 1/6 + 1 2/6

= 26/6
= 4 2/6
= 4 1/3.

mixed-up fractions
adding, say, 2/3 and 1/2, or 1/3 + 3/5,
or 1/5 and 3/8, or 7/20 and 7/12

adding two thirds to one half (2/3 + 1/2)

Using mixed-up fractions is a little more complicated, involving adding fractions like two thirds to one half: 2/3 + 1/2.

Starting with a simple example, a way of working out what is the common ‘bottom number’ of fractions in a sum is to lay out two rows of Cuisenaire rods, each row being made up of rods the length of one of the numbers being considered. For the sum 2/3 + 1/2, the two numbers would be 3 and 2.

Here you can see that three lots of two (red rods) is equivalent to two lots of three (green rods).

As you can see, one third of one is equivalent to two sixths, and one half is equivalent to three sixths. So we have two thirds, that is four sixths, and by adding the half, which is three sixths, we have seven sixths in all.

Thus,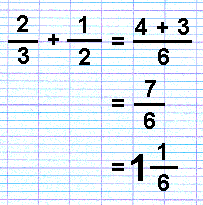

Looking back at the rod picture, you will see that the sixths go commonly into both the halves and the thirds. The sixths are the lowest common denominator, the biggest fraction that will divide into both the thirds and the halves. You will also notice that two times three equals six (2 x 3 = 6), thus multiplying the denominators together will give you at least one common fraction into which the fractions you wish to add may be divided.

adding one third to three fifths (1/3 + 3/5)

As you cannot add thirds and fifths as they stand, any more than you can add apples and oranges and end up with plums, you have to turn the apples and oranges into a similar purée in order to add purée to purée. So our first job is to purée the different fractions that we are trying to add together.

What we can do is turn the thirds into ninths or twelfths, or turn the fifths into tenths or twentieths, but we still will not be able to add them together efficiently.

So what we are trying to do is to find a way of cutting the thirds and the fifths into the ‘same’ size chunks as each other. This is what the search for a lowest common multiple is all about. It is, in fact, about finding the biggest bits (or fractions) that we can divide both thirds and fifths into evenly. So, in fact, in a way, this is the biggest common bits we can make of both thirds and fifths. Once again, we have some rather clumsy jargon.

Now let’s set about finding these biggest common bits (fractions) or, as the jargon says, the lowest common multiple. As you can see from the photo-diagram below, you can turn thirds into fifteenths and you can divide fifths into fifteenths! You can look at the yellow blocks as being fives, or as being five fifths; and the green blocks as being threes, or being three thirds. Or you can look at the stretch of fifteen white blocks as being fifteenths. As usual, the way you count depends entirely on your purpose.

As you can see in this diagram, both the fifths (5ths, yellow) and the thirds (3rds, green) can be turned into fifteenths (15ths, white), and so can be added together with ease. Instead of one third and three fifths, we now have three fifteenths and nine fifteenths, which total twelve fifteenths.

1/3 + 3/5 = 3/15 + 9/15

= 12/15

Ah, Eureka, as Eratosthenes’ mate Archimedes expostulated, leaping out of his bath and running down the main street in his excitement - well, actually, in his birthday suit. And as reporters of his day tell it, he wasn’t even arrested. It sounds like they had more sense in those days, or in ancient Greece.

But enough of this jollity, back to our search for biggest bits.

adding one fifth and three eighths (1/5 + 3/8)

So we are standardising two fractions which, in the real world, could both be portions of a cake (or anything else) divided into the same number of parts.

Supposing we have one part of, say, a cake cut into five portions, to be added to three portions of a cake divided into eight parts: 1/5 + 3/8. It would be easier if the cake was divided into the same number of portions for each fraction.

Here is another way of visualising such as sum, which is also another way of visualising the lowest common multiple, this time of 5 and 8:

Here we use a cross table to work out which is the smallest number into which both 5 and 8 will divide (their lowest common multiple). The highlighted crimson numbers show that 5 and 8 are both multiples of 40.

Using the cross table above (if necessary) to calculate the sum of 1/5 + 3/8
1/5 = 8/40 and 3/8 = 15/40.
(Five goes into forty, eight times. Therefore, one fifth equals eight fortieths.
Eight goes into forty, five times; and we have three eighths, which is fifteen fortieths).
So 1/5 + 3/8

= 8/40 + 15/40
= 23/40.

adding seven twentieths and seven twelfths (7/20 + 7/12)

Now looking back to the previous cases of 1/3 + 3/5, 1/5 + 3/8 and 2/3 + 1/2, notice that in each case we could find the biggest bits into which we can divide (split up) both fractions by multiplying the bottom numbers (denominators) together. So 3 x 5 gives 15ths, 5 x 8 gives 40ths and 2 x 3 gives 6ths.

Clearly, if we multiply 3 x 5, giving the result of 15, then 3 will go into 15 five times and 5 will go into 15 three times; and so on. But, as the numbers become bigger, it is sometimes thought helpful to continue to find the biggest bits that will go into each fraction, rather than deal in hundredths, or thousandths or seven thousand two hundred and twentieths (7,220ths) and onwards. Although, in these days of calculators and computers, we could really work work with whatever number that is obtained by multiplying any and all the denominators (bottom parts of fractions) together.

So now I am going to show you how your ancestors went about dealing with this problem in ‘the good old days’. For this next example, we will use the method of finding prime numbers of the bottom parts of the fractions, using the sum 7/20 + 7/12. Again, we are looking for the biggest bits (lowest common multiple) that go into both twentieths and twelfths.

We look for the prime factors of 20 and 12. To do this, start by dividing by the smallest prime factor you think will go until you run out of prime factors. I have an example here:

Now examining these prime factors, the separate prime factors that make up both 20 and 12 are 2 x 2 x 3 x 5. 2 x 2 is common to both numbers, so 2 x 2 needs to be used just one time in making the common biggest bit.

We could, of course, just multiply 12 by 20 and deal in 240ths, but this way we only have to deal in 60ths (2 x 2 x 3 x 5).

So now to write out the sum of 7/20 + 7/12 in the old-fashioned style:

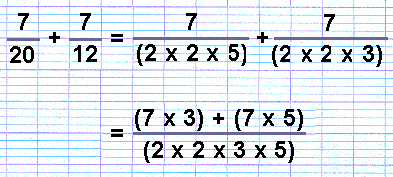
In the first line, the denominators (bottom parts) are expanded into their several factors.

In the second line, the denominators of the two fractions, 20 or (2x2x5) and 12 or (2x2x3), have been combined together (2x2x3x5). This results in the fraction 7/20, or 7/(2x2x5), being multiplied by 3 on the bottom part (that is, (2x2x5) x 3). So in order to keep this fraction balanced, we also multiply the top part by 3 (7x3).

1/(2x2x5) is 1/20, whereas 1/(2x2x5x3) is 1/60. There are, of course, 3/60ths in each 1/20. As there are 7/20ths in the original sum, 7/20ths therefore becomes 21/60ths.

Similarly with 7/12, or 7/(2x2x3), this fraction is multiplied by 5 at the bottom, so to keep it balanced we must also multiply the top part by 5.

Now the big combined fraction sum is simplified by doing the various multiplications inside the brackets, and then the addition.

cancelling

Tidying up and another form of balance.

As we saw briefly earlier, a half is equal to two quarters. You can easily see, dividing both the top and bottom of the fraction 2/4 by two gives 1/2, and of course, multiplying the top and bottom of 1/2 by two gives 2/4, thus maintaining the balance between the top and the bottom of the fraction.

As long as you multiply, or divide, both top and bottom by the same number, the balance will remain the same. As noted before, multiplication and division are opposites, or reverse (reversing) operations.

Fractions are are a form of ratio. Three-quarters is ‘three to four’ or ‘‘three out of four’. So as long as you keep the balance, for example six to eight’ or ‘twelve to sixteen’, the fraction does not change value and the ratio is preserved.

However, if you add, or subtract, the same number to the top and bottom of a fraction, so 1/2 becomes 2/3 by adding one to both the top and the bottom of the fraction 1/2, and the ratio or value is destroyed. [3]

Now some worked examples.

First 56/60, the result found for the mixed-up fraction addition, 7/20 + 7/12
7/20 + 7/12 = 56/60

The long way to cancel is to divide both top and bottom, 56 and 60, by 2 - the smallest prime number, until you can divide no more. Then, if it is possible, you continue with the next prime number. This is a bit like finding the biggest common bits (or lowest common factor).

As you gain more experience, you will perhaps notice straightaway that 56 and 60 are divisible by four (2 x 2).

Next let’s cancel down the fraction 12/15.

15 is not divisible by 2, so we start dividing both top and bottom with the next prime number, 3.

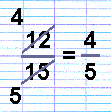
When cancelling down a number greater than one, turn the number into a fraction including a whole number (an ‘improper’ or top heavy fraction), and do the cancelling to that. For instance, in the addition sum 1/4 + 1 1/2 + 1 3/4, the sum is turned into 14/4, which cancels down to 3 1/2.

decimals

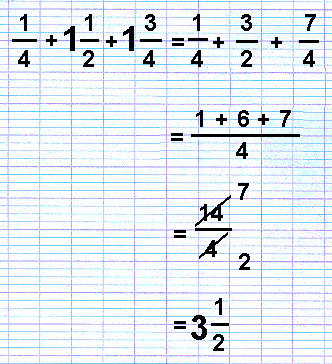
Until we reach putting in details in this section, 1/10 is written as ·1, that is a point (or dot) before the one, and one quarter is written as ·25, that is 25/100, and so on.

Adding decimals and subtracting decimals is no different from adding or subtracting any other numbers, beyond the necessity of keeping the decimal points lined up. It is easy to practise this with the calculator below.

Some examples:

• 2·43 +1·68 = 4·11
	To replicate this sum using the abelard.org maths educational counter, Reset Counter Value to 1·68; Set Decimal Places to 2; Change Step to 2·43; Switch Direction (if necessary) to Increasing; Now click on the Manual Step button once.
• 4 + ·09 = 4·09	When calculating with decimals, it is important to lay out the numbers with the decimal points lined up. In order to help the learner to keep clear in their own mind what is happening, it can be helpful to add extra zeroes, shown in the example to the left.
• 2·43 - 1·68 = ·75	This subtraction sum is handled like any other subtraction, as is explained in detail on the writing down sums page. Again, make sure that the decimal points are lined up as described above.

abelard.org maths educational counter

[This counter functions with javascript, you will need to ensure that javascript is enabled for the counter to work.]

The full version with more detailed instructions, go to the introduction page.

Thus, to practise sums with decimals, for example ·25 x 4,

• Reset Counter Value to 0;
• Set Decimal Places to 2;
• Change Step to ·25;
• Switch Direction (if necessary) to Increasing;
• Now click on the Manual Step button four times. The red number counts to 4.

The counter counts up: 0, ·25, ·5, ·75, 1. Thus ·25 x 4 = 1.

Now help the learner to try other multiplication sums. Each time, click the red Reset button to return Manual Steps (the red number) to zero.

Below is a concise version of the Brilliant abelard.org educational maths counter. For an expanded version with more detailed instructions, go to how to teach your child number arithmetic mathematics - introduction.

percentages

100% (one hundred percent) is a whole cake. 1% is 1/100th (one hundredth) of the cake.

1/10th (one tenth) is written as 10%, that is a percent sign (%) after the ten, and one quarter is written as 25% and so on.

nine one hundredths, or 9/100, or 9%, or ·9

fifty-six one hundredths, or 56/100, or 56%, or ·56

It is necessary to remain alert to the following facts:

• If you take 10% from one hundred, you end up with 90. 100 - 10% = 90.
  Whereas, if you now add 10% to 90, the result is 99, not 100. 90 + 10% =99.
  
  
• An increase of 10% in a population of 60 million is 6 million.
  
  Whereas, if you have ten pounds and it is increased by 10%, then all you gain will be one pound. Governments and advertisers constantly work to confuse people by taking advantage of the general lack of numeracy among the population. For example, governments will tell you that they are spending an extra £5 million on health services or schools, rather than tell you that £5 million is a very small fraction of 1% of the expenditure in these areas.
  
  But when government increases the number of helicopters for the military from 5 to 8, they will trumpet that they have raised the number of helicopters by 60%, while carefully omitting the real numbers of five and three more helicopters.
  
  Your advertiser of cat foods will tell you that eight out of ten cat owners said that their cats preferred Kattosludge (boiled meat factory waste), while failing to tell you that the cat owners worked for Kattosludge Incorporated, and only ten owners took part in the survey.

Adding percentages and subtracting percentages is no different from adding or subtracting any other numbers, or fractions (remember that 1% is one hundredth of something).

For more advanced compound percentages/interest rates, see the sum of a geometric sequence: or the arithmetic of fractional banking (compound interest).

ratios

Ratios are very similar in behaviour, but can be used rather haphazardly. For example, 3:1 (three to one) can mean that for every one apple there are three oranges. Notice that in such usage, there are four real objects, the three apples plus the orange.

Another usage is in betting, where you may may have odds of four to one. This tends to mean that you bet one pound, dollar or euro in the hope of winning four sponduliks back for every one you lay out. Usually, if your horse or camel wins, the bookmaker will pay you both the four zelottis for your winning plus the one zelotti of your original bet. This sort of bet is often termed as “four to one against”.

If the ratio is expressed the other way about, that is 1:4, it is referred to “four to one on”. In other words, for every four you bet, you will gain one and, of course, receive back you stake of four. So you receive five for an outlay of four - if you win. These are the sort of odds you are offered if you have a very good chance of winning, or even too good a chance of winning.

It is always wise to be very clear on definitions when ratios or percentages are being quoted, and to remember that most gambling is a tax on stupidity.

rounding numbers

Farmer asks his dog to get the sheep in. The dog goes out, comes back and says I've got them. Farmer says have you got them all? Dog says I've got 40. Farmer says I've only got 36. Dog says I've rounded them up.

There are times when you don't want to refer to a number, because it is very large like 6,303,589,102, or a decimal like 3.14159265358979323846264338. In such cases, the number can be changed to a simple number of a value close by.

Because we use the decimal system, our culture tends to round (change) to the nearest appropriate number ending in zero - to ten, a hundred, a thousand etc.
The general convention used for rounding is,

If the last digit is 4 or less, the complete number is rounded down to the nearest number ending in zero.
For instance, 5.1 would be rounded down to 5.

If the last digit is 5 or more, the complete number is rounded up to the nearest number ending in zero.
For instance, 5.6 would be rounded up to 6.

In the examples we gave, 6,303,589,102 could be rounded to 6 trillion or 6.3 billion, depending on the degree of accuracy wanted.
3.14159265358979323846264338 is an partially expanded version of π [pi]. A usual rounding is 3.14.

Sometimes, often when doing sums at school, it is required to give a decimal number to a certain number of decimal places.
So 3.14159265358979323846264338 is an approximation of π to 26 decimal places, while 3.14 is rounded to 2 decimal places. 3.1416 is π to four decimal places. Here, the fifth decimal place (9), being bigger than 5, signals rounding up the fourth decimal place (5) to 6.

Note that this makes the number concerned less accurate, an approximation.

end notes

1. Be aware that fractions can be written in more than one style. One style is thus, ½, and another is 1/2. A third style is
   .
   And of course, 1 ÷ 2 also has the same meaning.
   
   
2. The technical names for the parts of a fraction are:
      numerator
   —————
    denominator.
   
   The numerator is sometimes called the dividend, while the denominator is also called the divisor.
   When the top part of the fraction (the numerator or dividend) is smaller than the bottom part (the denominator or divisor), strangely and historically the fraction is called a ‘proper fraction’. A proper fraction is always of a value that is less than one.
   When the numerator or dividend is larger than the the denominator or divisor, the fraction is weirdly called an ‘improper fraction’.
   
   
3. In another page dealing with equations, you will see equations, that is sums arranged either side of an equals sign, where balance is maintained as long as the same is done to both sides - add, subtract, multiply, divide or whatever. Whereas, with fractions, the balance is maintained only by forms of multiplication and division.
   
   
4. The nomenclature widely and normally used for fractions is illogical and confusing. How you wish to deal with this, I will leave to you. The common usage is to call numbers of the form 1 1/2, where there is both a whole number and a fractional part of a number a ‘mixed fraction’.
   
   Often it is useful to handle such numbers by putting it all into fractional form. Thus, with 1 1/2, the 1 is broken into two halves and added to the remaining half. Thus 1 1/2 becomes three halves or 3/2. And this type of fraction is foolishly called an ‘improper fraction’.
   
   Remember, I wish that people be taught in a realistic and meaningful manner using sensible language. There is nothing improper about a fraction valued at over one. Neither is there much mixed about that same fraction expressed when expressed in the form 1 1/2. The so-called mixed fraction, or the so-called improper fraction, are essentially numbers pointing to values in the real world.
   
   Meanwhile, teaching fractions etcetera proceeds in a logical order from simple fractions, such as 1/4 + 1/4, then moving onto numbers that include whole numbers, such as 1 1/4 + 1/4, and finally moving onto actually mixed fractions such as adding 1/4 +1/5. But if I call these last examples mixed, as is logical, the learner is likely to become confused when meeting teachers that use clumsy language or jargon.
   
   With children who are coping well, I teach learners logically and warn them that they will very probably come across people using the clumsy jargon. I explain to them how this jargon is used, while telling them not to worry much about it, just learn enough that they remember how the jargon is used when they run across it in classrooms or in exams. In the body of this page and on other pages, I shall primarily use clear and sensible terms.
   
   
5. It is common to put a zero before the decimal point (dot), as in 0·1. As people become used to mathematics, they tend not to put the zero in front, as it has no meaning any more than they tend to put a zero after a number like 1 or 15, as in 1·0 or 15·0. But it is common, at times, to use leading or trailing zeroes in lists of figures.
   
   However, given that most calculators, including those on computers, automatically include a zero in a sum such as ·3 + ·5, you may have difficulty in convincing others that the zero before a decimal point is unnecessary and should not really be there.
   
   the decimal point
   On these sums pages, generally we display the decimal point in the middle of the numbers, for instance 1·7. However, because doing this requires a special character, both in print and on a computer, nowadays, the decimal point is frequently displayed as a full stop/period: 1.7. (In continental countries such as France, a comma is used as the decimal marker: 1,7, while the thousands marker is a space: 2 200 or, sometimes, a dot: 2.200.)
   
   
6. This method will work just as well when adding or subtracting three or more mixed-up fractions.

email email_abelard [at] abelard.org

© abelard, 2009, 1 may

all rights reserved

the web address for this page is https://www.abelard.org/sums/teaching_number_arithmetic_mathematics_fractions_decimals_percentages1.php

5,840 words
prints as 23 A4 pages (on my printer and set-up)