site map

sums will set you free

how to teach your child numbers arithmetic mathematics

writing down logarithms

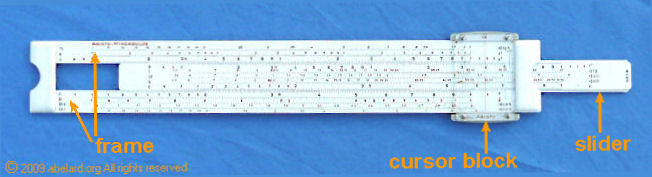
Logs (or logarithms) to base 10 are normally written as log. Logs to other bases are written as log₂ for logs to base 2, or log₅ for logs to base 5, and so on. It is important that the number indicating the base of the logarithm is clearly written as smaller and below the word ‘log’, otherwise log₂ might be confused for log 2, a very different animal.

tools to help working out logs

In the 1600s, Napier invented logs. Briggs created useable log tables (we will look at these a little later).

From early on, slide rules were developed, and were used widely for science and engineering calculations until the advent of computers and pocket calculators.

slide rules

Below is a scientific slide rule.
When closed, it is 337mm long and 46mm deep. The cursor block is 59mm deep.

advertising disclaimer

This linear slide rule is set to do a simple calculation - 3 x 2.

The central slider is moved so its number 1 is aligned with the 3 on the upper half of the frame. The left orange diamond in the enlargement below highlights this.

The 2 mark on the central slider lines up with the 6 on the outside frame. So this sum’s answer is 6 (highlighted by the right orange diamond), but why?

Remember that a slide rule is physical version of doing calculations using exponents, or logs. With our sum of 3 x 2, we take the length equivalent to log 3 on the outside frame and add to it the length equivalent to log 2. The resulting combined length is the equivalent to log 6. So although we have added together two lengths, the result is the equivalent of multiplying two numbers.

With the slide set in this position, you can do further calculations such as 3 x 3, or 3 x 2·5 (= 7·5).

As well as linear slide rules, there are (or were, if you believe these tools to be redundant antiques) circular slide rules.

Here is a photo of one, pretty isn’t it?

Instead a frame and a slider, there are inner and outer rings that can move separately. You can just see the transparent cursor block, that can rotate around the slide rule’s centre point. This slide rule has a diameter of 12.3 cm.

As with the linear slide rule we show just above, this slide rule has been set to to show a simple multiplication sum, again 2 x 3 = 6.

On this circular slide rule, the starting points for the different log lengths are marked with a triangle.

• The triangle on the outer ring (highlighted within the orange diamond) is pointing to the start of the log scale for the first number, 2.
• The triangle for the inner ring (highlighted within the blue diamond) is set to the length that is the equivalent to log 2.
• The cursor, marked with an orange arrow (the two outer arrows show the extent of the transparent cursor block), is placed to the length equivalent to log 3 on the inner ring (highlighted in the green diamond). As you can see, the cursor indicates how the 3 also lines up with 6 on the outer ring.

With the slide set in this position, you can do further 2-times calculations: 2 x 4 = 8, 2 x 5 = 1 (!). For this last sum, you have to use your intelligence and realise that the zero is not shown, as 2 times 5 equals 10.

advertising disclaimer

log tables and how to use them

Log tables generally come in small books, including as well as log tables, tables for calculating other variables such as cosines, cosecs, cotangents and anti-logs - used to convert a log number back into an integer.,

A bit further down this page are part of four-figure (four-place) log tables. They are used for doing multiplication and division sums using decimal numbers with up to four figures after the decimal point. (There also links to full full log tabbles that uou can print out to use.)s

Before using the tables, you need to understand some things about them. First be aware that although there is no decimal point in the log tables, the groups of four numbers are decimal fractions.

Next, log tables are designed to save space, so the size of the number is separated from its value. What does all this mean? Well, instead of having separate tables for say 1 to 100, 100 to 1,000 and 1000 to 10,000, there is one set of tables, and the user - you - indicate afterwards the size of the number.

So a log number is split into two parts: to the left and to the right of the point. The part to the left is called the ‘characteristic’, and indicates the order of the log

if the number comes between 0 and 10, say 1·2, its log must lie between 0 and 1: the log will be 0.something;
if the number comes between 10 and 100, say 12, its log must lie between 1and 2: the log will be 1.something;
if the number comes between 100 and 1,000, say 120, its log must lie between 2 and 3: the log will be 2.something;
if the number comes between 1,000 and 10,000, say 1,200, its log must lie between 3 and 4: the log will be 3.something.

Note that in each case, the characteristic is the same as the index (or exponent) when the number concerned is expressed (written) as a number to a power of ten: 10⁰, 10¹, 10², 10³.

And the something, the part to the right of the point?
This is always the same number for same digits, no matter where the decimal point may fall. It is called the ‘mantissa’, and is worked out using the log tables, like those shown just below. [The numbers in boxes are part of the working for converting an number into a base ten logarithm, which is described just below.].

Click for complete, unmarked, four-figure log tables to print out. [Opens in new tab/window.]

Click for .pdf version of complete four-figure log tables to print out.

converting a number into a base ten logarithm

Now to do a sum using log tables. Suppose you want to multiply 24·78 x 33·16. We start by working out the mantissa, the part to the right of the decimal point in the log,
[On the page of log tables above, the numbers in boxes are part of the working for this sum.]

For 24·78,

• first, look for 24 in the N column, then run your finger across to the 7 column. Note (with your finger, or memory) that the number there is 3927.
• Keep moving your finger on the same line until you reach the 8 column of “the proportional parts”. Note the number there is 14.
• Add together 3927 and 14 for the mantissa of the log of 24·78: 3941.

This mantissa is added to the characteristic of 24·78 to give the log.

• Because 24·78 is between 10 and 100, its characteristic is 1.
• So the log of 24·78 is 1.3941. Log 24·78 = 1.3941.

For 33·16,

• first, look for 33 in the N column, then run your finger across to the 1 column. Note (with your finger, or memory) that the number there is 5198.
• Keep moving your finger on the same line until you reach the 6 column of the “Proportional Parts”. Note the number there is 8.
• Add together 5198 and 8 for the mantissa of the log of 33·16: 5206.

This mantissa is added to the characteristic of 33·16 to give the log.

• Because 33·16 is between 10 and 100, its characteristic is 1.
• So the log of 33·16 is 1.5206. Log 33·16 = 1.5206.

Now, 24·78 x 33·16 being a multiplication sum, the two logs are added together.
1.3941 +
1.5206
2.9147

2.9147 is a log to base ten - that is, it is 10^2.9147.
This log needs to be converted back into a number to find the result of our multiplication sum.

 resolving a base ten log to a number

Well, this can be done using another set of tables called anti-logarithms, but here we are going to be tough and numerate, and use the log tables themselves!

• First we disassemble the log into its characteristic and mantissa: 2 and 9147.
  The characteristic of 2 we will ‘put aside’ to use later.

  Now to the mantissa, 9147!

• Looking at the log table below, we find the number that equals or is slightly smaller than 9147.
  On the line for 82, in column 1, is 9143.
• So we go along the line, to the right, until we find a 4 in the Proportional Parts section (9143 + 4 = 9147).
  
  To add to the fun, this time we find 4 twice, in the 7 and in the 8 columns. This is because the tables are only for four places of logarithms, and so sometimes rounding errors come in. In our case, we now know that the fourth place in our resolved number is somewhere around 7 and 8, so we will take an average of 75. (Note that we ignore any decimal places until we apply the characteristic to the completed/resolved mantissa.)

So the mantissa resolves to 82175.

• But remember the characteristic that is 2, that we’d ‘put aside’?
  A characteristic of 2 means that the number from which the log is derived comes between 100 and 1,000.
• So the original number (that has a log of 2.9147) comes between 100 and 1,000. Thus, the resolved number must be 821·75, or 24·78 x 33·16 = 821·75.

Checking by calculator, the result of 24·78 x 33·16 = 821·7048. Remember that we have been using four-figure logs, so small inaccuracies will creep in.

So this is the way they used to do it in the olden days, with logs as a short cut (of course, you become a lot faster with practice), or with much faster, but less accurate, slide rules. There are logarithm and other tables going up to ten figures, and probably beyond, which can be useful for checking out computer programmes. And of course, computer programmes can now generate such tables through various iterations.

Now you have your handy pocket calculator, you may think that calculating with logarithms is a bit tiresome. But remember, understanding the processes involved is very useful in building a foundation in understanding how numbers and indices/powers work.

You notice that there all sorts of other scales on the slide rules shown above, allowing you to look up many other interesting ratios and results. Similar look-up tables are generally available in log table books.

logs of a number between zero and one: the bar characteristic

When a number between zero and one is converted to a base 10 logarithm, log₁₀, the characteristic of the log (like the power of a number to base 10) will be negative. That is, while a log’s mantissa is always positive, its characteristic will be negative for numbers that are less than 1.0.

When writing by hand, it is easy to write a negative characteristic as it should be, with a line - the bar - above the number. Unfortunately, typical computer keyboards (as well as calculators and modern typesetting) cannot make a mark like this, so a negative characteristic is very often shown as a minus sign before the characteristic. Because we are also limited by computer typesetting capabilities, we also will put a minus sign to indicate a negative characteristic - a bar log. This is what a log with a negative logarithm looks like when hand-written .

When you write down logs, you can either write them like this example, or you can write them as a calculator or computer does - if you are sure than you will not become confused. Remember the characteristic can be negative or positive, but the mantissa (to the right of the point or dot) is always positive.

Now this can easily cause confusion because a minus sign in front of a decimal number, such as -1·234 (or nowadays frequently written/typed as -1.234) applies to all the numbers in the decimal: our example decimal number is made up of -1 and - ·234.

A log that is described in words as bar one point two three four, and written as -1.234, is made up of a characteristic of -1 and a mantissa of .234, not -.234.

Here is an example sum: 3 x ·09.

Using the log tables above,
the logarithm of 3 is 0.4771,
and the logarithm of ·09 is -2.9542, , or bar 2 and .9542.

Since 3 x ·09 is a multiplication sum, the two logs are added together.
 0.4771 +
-2.9542
-1.4313

Disassembling the log into its characteristic and mantissa: bar 1 and 4313.
The characteristic of -1 we will ‘put aside’ for later use.
Using the log tables above, the mantissa resolves to 2699.

Now we use the characteristic of -1 to determine the size of the resolved number. A characteristic of -1 means that the number must be between ·1 and ·9. So the resolved number must be ·2699.

Again rounding errors have crept into our calculation using logs. Doing this sum directly, the answer is ·27.

multiplications involving negative numbers

When multiplying negative numbers, we would carry on as if the numbers were positive and then, at the end of the multiplication, we would correct the final result using the usual rules. That is, positive times positive or negative times negative give a positive result, while negative times positive and positive times negative give a negative result; or, same signs positive, opposite signs negative. This can be expressed in a typical binary table:

divisions using logs

For divisions using logs, analogous procedures apply. For a - b (for instance, 3 - 2), the log of 2 will be subtracted from the log of 3. Otherwise, continue as usual. You can also see this process on the slide rule above, where 3 x 2 = 6 can also be read in reverse where 6 ÷ 2 = 3.

logarithms and exponentials - ta.s.

A logarithmic relationship is the reverse of an exponential relationship. In an exponential relationship, things get bigger faster and faster. In a logarithmic relationship, things get bigger slower and slower.

For example, the following equation describes the simplest exponential relationship:-

y = 10^x (1)

As x gets bigger, y gets bigger and y gets bigger faster and faster. Any positive feedback system, like a nuclear explosion, can be described by an exponential relationship.

x = log₁₀ y (2)

Equation (2) means exactly the same as equation (1), except this time we care more about what happens to x. As y gets bigger, x gets bigger, but x gets bigger slower and slower. Equation (2) describes a logarithmic relationship. Any negative feedback system, like the way your body regulates your temperature, can be described by a logarithmic relationship.

Every exponential relationship can be looked as a logarithmic relationship, and vice versa.

Mathematicians often use a special number called ‘e’ (~2.72), instead of 10:

y = e^x (3)
x = log_e y = ln x (4)

e is used because it has some special properties that make the sums in calculus - mathematics for calculating the slopes of curves and the areas under curves - easier. The logarithm base e is sometimes called the “natural logarithm” and written as “ln”. When the base of the logarithm is not made explicit, for example “y = log x”, it is assumed to be a base 10 logarithm, as in equation (2).

end notes

1. The dot, looking like a full stop, that separates the characteristic of a logarithm from the mantissa to the right, is called “point”. It is similar to the decimal point, but is not the precisely same. Remember that a decimal point should be on the mid-line of a number, but like a full stop, the logarithmic point lies on the base-line of the number.

email email_abelard [at] abelard.org

© abelard, 2009, 24 november

all rights reserved

the web address for this page is https://www.abelard.org/sums/teaching_number_arithmetic_writing_down_logs.php

2615 words
prints as 10 A4 pages (on my printer and set-up)