
dividing - division - in balance

In equilibrium - five blocks on each side
 |
 |
| if only one side is
divided by five, the equation becomes unbalanced |
dividing each side by
five, there is equilibrium |
At times, making sure that the two sides are in balance
can be complicated, but you always have a remedy - check
what you are doing with small numbers and see whether
the two sides are, in fact, still in balance after your
actions.
constants
and variables
Numbers can be referred to as constants.
When we don’t know what a number is, a variable can be used.
That is, we know there is a number, but we don’t
yet know what it is. All manner of symbols can be used
for variables, usually starting with the lower case alphabet,
but eventually you may come across Greek letters, German
gothic letters, made-up symbols, or even words. So x,
y, teacup, or pink balloon could all be used as variables.
While it is common to talk of constants and variables,
it is important to realise that
constants are also a form of variable. ‘One’
can mean one elephant, one galaxy, or the one drawing
pin you just sat on. Always remember, there is nothing
‘special’ about numbers. They are just more
words used by humans as they seek to commmunicate about,
and to become masters of, the known universe.
BODMAS
and simplifying, or rationalising, equations
Before immersing yourself in this section,
you might want to study, or re-study, any or all of the
following pages:
Equations often will include several variables and operations.
(Operations are actions done to numbers and include adding,
subtracting, dividing, squaring - multiplying a number
by itself.)
Supposing you have the following equation, (2 + 5²
- 1/4) ÷ 3 = x, and you
want to find the value of x.
Yes, you can work it out using lots of blocks but that
takes quite a while and isn't very convenient a lot of
the time. So what to do, where to start with teasing out
a value for x.
This is where BODMAS comes
in, an acronym for
Brackets, Orders, Divide and Multiply, Add
and Subtract.
This is the order of actions to take when resolving a
more complicated equation. Other than this order, you
go from left to right along the equation/sum. Note that
division and multiplication rank equally, as do addition
and subtract.
So for (2 + 5² - 1/4) ÷ 3 = x
- First work out the sum within any brackets, here (2
+ 5² - ¼).
- Next come orders: these are powers or exponents.
Within the brackets, checking through the sum you see
that there is a number that has a small 2 by it. 5²
is five to the power of two, the 2 is an exponent, and
5² means five squared, or five multiplied by itself:
5 x 5. 5² = 25.
- There are no divisions or multiplications with in
the brackets, so going from left to right, 2 + 25 =
27; 27- ¼ = 26 ¾.
- Next there is the part of the equation (or sum) outside
the brackets: ÷ 3. So 26 ¾ ÷ 3
= x.
- Before going further, it is more usual to put the
unknown variable x on the
left side of the equation, x is the thing we are really
concerned with so, as in an sentence, ‘the cat
is big’ not ‘big is the cat’, we rearrange
the equation and write x =
26 ¾ ÷ 3.
- Now back to calculating x,
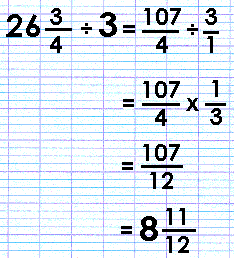
- Thus x = 8 11/12.
the
beginnings of algebra
No, algebra is not particularly complicated. Instead
of using numbers, you merely use letters or combinations
of letters and numbers, or should that be numbers and
letters.
Note that, in algebra, 2 x a is written as 2a. Another example
is 3 x a is written as 3a.
7b is the same as 7 x b.
Thus two blocks equals two blocks, and a = a, and 2b = 2b.
So if a = 2, you will immediately
know that 2 = a, and 2a must
equal 4. That is 2a = 4.
But you may start off not knowing what a is. a may equal 6 - 3, when
it is obvious that a = 3.
Or you may have two equations, one telling you that b = 3c,
and the other that c = 4.
So you can see that 3c = 12,
and therefore b must equal 12.
Putting the value of c into
the equation b = 3c is called substituting,
the value of c is substituted
into the equation.
Believe it or not, by this time you are already doing
simultaneous equations (two equations and one ‘unknown’).
Here are some simple algebraic sums:
- 2 + b = 7
b = 7 - 2 [2 is subtracted from each side of
the equation]
= 5
- 2 - b = 7
2 - b + b = 7 + b [b is added
to each side]
2 = b + 7 [ - b + b leaves nothing, or zero]
2 - 7 = b
b = 2 - 7 [the equation is reorganised so the
variable b is on the left]
b = -5 [the last two steps could have been done
together]
- 2 x b = 7 [or 2b = 7]
b = 7/2 [divide both sides
by 2]
b = 3 1/2
- 2 ÷ b = 7
2 = 7 b [multiply both sides by b]
2/7 = b [divide both sides
by 7]
b = 2/7 [the equation is reorganised
so the variable b is on the
left]
They call this sort of thing simplifying equations. The prime objective is usually to isolate one
element of the equation and express [describe it] it in
terms of the rest of the equation. As has already
been discussed, the important thing is to keep the
equation in balance.
isolating
elements and nicely complicated equations
The next section takes two nicely complicated equations
and shows you how to isolate one element. This is called
transformation - you tranform an equation from say, a
+b = c, into a = c - b.
You might think that I would build up through lots of
simple equations, but this way, you will see just about
every trick in the book applied to isolating an element,
while maintaining the balance of the equation. If you
can tackle these two, you can approach almost anything
with confidence and fun. This is the way I go about such
things, but some people may prefer to go slowly through
myriads of graded examples, climbing step by step up the
stairs. Here, we go up the lift and balance out of the
high wire!
Remember, it’s all about balance. What you must
do is to keep rigorously to the rule that, “what
you do to one side, you must do to the other side”
- and not to part of one side, but to the whole of the
side.
how
to transform equations 1 - the pendulum equation
An equation can be thought as, for instance, a shorthand
question about a particular (scientific) situation. For
instance, if a string is 10 cm long, how quickly will
a pendulum swing? But sometimes the equation, or shorthand
question, has the wrong object as the subject of the sentence.
Maybe you know how fast the pendulum is swinging, and
you want to know the length of the string. Here the question
has been rearranged. But to calculate the value of one
variable (string length, pendulum swing time), the mathematical
sentence, or equation, will have to be rearranged. Finding
the answer you want is called ‘transforming the
equation’.
Take the Pendulum Equation. This equation describes mathematically
how long a weight on the end of a string (the pendulum)
takes to swing back and forth once (its period of oscillation).
how a pendulum swings
When a pendulum bob is moved from the vertical, the the
force of gravity pulls the bob downwards - it tries to
drop (remember Galileo dropping weights from the leaning
Tower of Pisa?).
But the pendulum cannot go straight down because it is
constrained by the pendulum string. When the pendulum
reaches its lowest point, where the pendulum line is vertical
again, it cannot stop immediately. There is enough energy
for the pendulum to keep moving. And it does so until
the pull of gravity is equal to the energy in the moving
pendulum. At this point, the pendulum falls back earthward.
This we see as the pendulum swinging back and forth. If
there is no friction where it is attached to its suspension
point and there is no wind resistance to the pendulum’s,
this would continue forever.
Here is the simple
form of the Pendulum Equation: 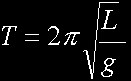
sorting out equation gobbledygook
Now this equation may look like gobbledygook, but we will
translate this equation so it makes sense in English.
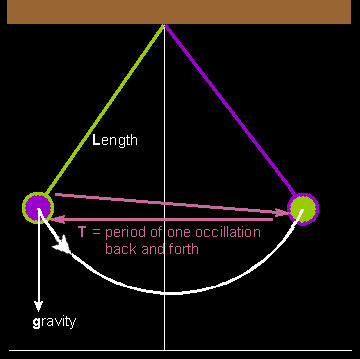 Each letter stands for one of the variables in how a pendulum
moves. In the simple pendulum equation, the bob (the lump
at the end of the string that swings) is assumed to have
no mass. Each letter stands for one of the variables in how a pendulum
moves. In the simple pendulum equation, the bob (the lump
at the end of the string that swings) is assumed to have
no mass.
T = period in seconds. The
period is the time taken during for one full swing, or
oscillation, of the bob back and forth. The bob moves
away from its starting point and returns to it.
L = length of the pendulum
arm [or string] in metres.
π = the constant pi, whose
value is 3.14159... and
so on. Pi is used in geometry calculations involving
circles and arcs.
g = acceleration due to gravity.
An average value for g on Earth is 9.81
m/s².

And now let’s delve into the nitty-gritty of the 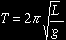 equation. equation.
- If you look carefully, you will see that the period T depends directly on the
length L of the pendulum -
as L becomes larger, so does T.
- On the other hand, because g is at the bottom of the fraction (or division)
doing the dividing, as it becomes bigger, the period T becomes shorter. And in
the real world, if g is greater,
the pendulum will fall faster, and so T will be less.
- Overall,
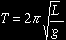 does not have a linear relationship - that is, it cannot
be used to make a
straight line graph - because there is a square
root in the equation. This information is useful
should you want to rearrange the equation. does not have a linear relationship - that is, it cannot
be used to make a
straight line graph - because there is a square
root in the equation. This information is useful
should you want to rearrange the equation.
isolating an element from the
apparent mess (transformation)
Now looking at this apparent mess, which is the most difficult
element for us to extract? Suppose you’re interested
in the length of the pendulum string can be, for it to
take a certain time to swing back and forth (to oscillate
in a certain time period). To find this out, you will
have to rearrange the equation so that the length, L,
is to the left of the equals sign and the rest of the
equation is on the right. Yes, L looks a good candidate to me. If we can tease out L,
we can tease out anything. So how the blazes are we to
dig L out of bag of goodies?
We rearrange the equation. This takes are a number of
steps.
First the step is described, and then we show how the
equation is affected:

And here follows the more orthodox method of rearranging
this equation. abelard is of
the opinion that it is not so easy to understand:

how
to transform equations 2 - the resistor equation
The resitor equation is another tricky mathematical animal
to tame. But why is there a
resistor equation, and why on Earth someone might want
to use it? Here is some fairly easy explication, but you
can skip it if your head starts to go fizz.
first, what is a resistor?
A resistor is an electrical element found in almost
every electronic circuit. Resistors, as the name suggests,
impede current flow and they are used to control the way
current courses through the circuit. Their resistance
is measured in ohms (symbol Ω). Because most resistors are too small
to display figures or letters, their ratings are displayed
by colour-coded
bands.
The behaviour of an ideal
resistor is defined by Ohm’s law, “current,
I, is directly proportional to voltage, V, for a metal
conductor, R, at a constant temperature”, or mathematically:
I=V/R [we have rearranged Ohm’s law, V=IR, to match
the definition just given]. Ohm’s law will be referred
to later on when we explain the resistor equations (yes,
there is more than one version).
Resistors can be combined by connecting together in in
series or in parallel, or in a combination of these ways.
This can be helpful if you do not have a resistor of the
exact value needed as the values combine..
Often, when building electronic (or electrical) devices,
it is necessary to calculate the voltage, or the current
being used, or the resistance in the circuit, so that
the electronic elements both work, and do not burn up
and fail. The resistor equation is used to find out the
combined resistance of several resistors in a circuit.
connecting in series
This is when resistors are linked one after the other,
in a series. 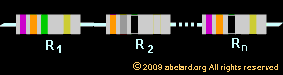
Their total equivalent resistance is found by the equation,
Req = R1 + R2 + ...
+ Rn . Finding the value of one of the resistors
in the circuit is just a matter isolating that resistor
by subtraction.
Thus, to find R1 in the equation Req = R1 + R2 + R3, subtract
R2 + R3 from each side :
Req - (R2 + R3) = R1,
or R1= Req - R2 - R3.
connecting in parallel
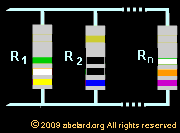 Resistors
which connected together so they are in paralleleach have
the same potential difference, or voltage. To find their
total equivalent resistance, this equation is used: Resistors
which connected together so they are in paralleleach have
the same potential difference, or voltage. To find their
total equivalent resistance, this equation is used:
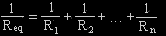
Now supposing the circuit has two resistors in parallel,
the equation will be 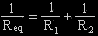 . .
Find R2, what is R2?
Now this is quite tricky to do, we use several mathematical
tools which have already been described on other related
pages at abelard.org. The mathematical
tools are highlighted here in yellow,
if you click on them you will be taken to the relevant
section of that page.

end notes
- Orders
are also referred to as indices.
- Division can be described using
‘of’. For example, four of five is four
fifths, 4/5.
- There are more complicated
versions of the pendulum equation that use concepts
like calculus for more detailed calculations of the
behaviours of a pendulum, such as its velocity. More
complicated versions may also take into account things
like the angle from the perpendicular at which the bob
is released.
- Pi (π is the Greek letter equivalent to P) is a mathematical
constant that can be defined as π
= C/d, where C is the
circumference of a circle and d is its diameter. Pi is an irrational number, that is
it cannot be expressed (or written) exactly as a fraction a/b, where a and b are integers; pi cannot
be written as a ratio. Thus the decimal representation
of pi, which starts 3.14159 26535 89793 23846 26433
83279 50288 41971 69399 37510… [pi to the first
fifty decimal places], never ends or repeats. Pi has
been calculated, so far, to more than a trillion (1012)
decimal places. However, for most calculations, just
a few decimal places are sufficient. 22/3 is a common
fractional approximation for pi.
- We are using metric units as values
for the different variables - L in metres, T in seconds,
g in metres per second squared (m/s²). The imperial
equivalent is to describe L in feet and g as 32.2 ft/s.
- One ohm is the resistance value
through which one volt will maintain a current of one
ampere.
Power is measured in watts, voltage in volts, current
in amperes - amps for short, and resistance in ohms.
-
 Resistor ratings are usually coded with four bands:
bands A and B the significant figures of the resistor’s
value, band C is the decimal multiplier, and band D,
if it is included, shows a tolerance value as a percentage
(no color means a tolerance of ± 20%). The following
is an abbreviated version of the colour coding. Resistor ratings are usually coded with four bands:
bands A and B the significant figures of the resistor’s
value, band C is the decimal multiplier, and band D,
if it is included, shows a tolerance value as a percentage
(no color means a tolerance of ± 20%). The following
is an abbreviated version of the colour coding.
| |
black |
brown |
red |
orange |
yellow |
green |
blue |
violet |
grey |
white |
gold |
silver |
| significant figure |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
| multiplier |
x 100 |
x 101 |
x 102 |
x 103 |
x 104 |
x 105 |
x 106 |
x 107 |
x 108 |
x 109 |
x 10-1 |
x 10-2 |
| tolerances |
- |
± 1% |
± 2% |
- |
- |
± 0.5% |
± 0.25% |
± 0.1% |
± 0.05% |
- |
± 5% |
± 10% |
Thus, the resistor illustrated above is rated as 73
x 105 Ω, or 7,300,000 Ω, with a
tolerance of ± 5%.
Notice that the colours from red to violet are the colours
of a rainbow, where red has low energy and violiet higher
energy!
And here are some other resistors, so you can work out
their ratings:
   
- In the real world, resistors
can heat up, burn out, or have other problems, as well
as not having perfectly linear behaviour - their resistance
may be consistant with different current, voltages.
On the other hand, in a ideal, or perfect, resistor
the resistance remains constant regardless of the applied
voltage or current flowing through it, or the rate of
change of the current - the perfect resistor has linear
V vs I behaviour.
|



















