site map

sums will set you free

how to teach your child numbers arithmetic mathematics

writing down sums

The approach to teaching mathematics and other languages is profoundly unsound, but the habits are deeply ingrained.

I have already provided documents explaining where the problems are on a technical and adult level. To dig into this, start at why aristotelian logic does not work and laying the foundations for sound education.

This sub-section of abelard.org is designed to lay out a rational and logical base for teaching arithmetic and mathematics from basics. I shall not always justify the methods in this section as I go along, but the methods are very relevant and purposefully structured. Throughout this section, many of the yellow links take you to a more advanced, or technical, explanation.

It is vital to understand that there is no fundamental or logical difference between the symbolism of teaching English and teaching arithmetic/mathematics. This congruence becomes part of the learner’s understanding. It is a deep and dangerous pedagogical error to allow the learner to imbibe the erroneous concept that mathematics and English are different “subjects”.

On these pages, you will be given basic methodology and necessary examples. You will not be provides with hundreds of examples, those you make up as you work with the learner, adjusting those examples according to the person’s problems. Some examples should be interspersed which are easy for the learner, in order to reinforce and to give experience of success, while others should be aimed at specific difficulties.

writing down sums

• Divide the page into two, not necessary equal, parts (we used to rule a line from top to bottom of the page, but there is no reason not to make a horizontal dividing line).
  Keep one side for the ‘good’ work where everything is written as neatly and clearly as you can, and the other for making as much mess as you like with the ‘rough working’ for intermediate calculations, and developing your own calculating methods. Note, it is generally sensible to keep the rough working fairly tidy, so the origin of any error can be discovered more quickly when you check the calculations.
  The ‘clean’ side is where you make sure you have not got in a muddle or made any silly mistakes.
• Keep the sum in a column, or two columns if there are collections of tens as well as collections of units (less than ten objects).
• Put the sign for what sort of sum it is on the left of the second items, then later you know on which sort of sum you were working.
• Put two horizontal lines to separate the answer/result of the sum. This helps to keep the numbers organised. It also provides a position under the lower line for any further working, such as numbers being carried forward from the units to the tens column.
• For those starting writing down sums, it is helpful to put labels above the two columns : T (for Tens) and U (for units). For ‘bigger’ sums, there could be also H (for hundreds).

writing down addition sums

Addition with units, such as adding together a collection of two things and another collection of three things.

Addition sums can be written in a horizontal row, 2+3=5. Another way is to write them in a column.

	2
+	3
	5

This method ensures consistency when adding collections of things that add up to more than nine, or that include collections of more than nine items, for example 4+7=11 or 13+8=15. The collection of ten is written in a second column to the left, the tens column (T for short).

	T	U
		4
+		7
	1	1

In the following sum, fifteen things, or ten plus five things, are added to eight things. When the five and the eight things are added together, the result is a group of ten things and a group of three things (which is thirteen things in all). The ten that is part of the collection of thirteen things is written below the total of the tens column, and then added to the one ten that is part of the group of fifteen things. [As a child, I learnt the ‘mantra’, “put down three (or what ever is the units in the summation) and carry one”.] Here, the one that is carried is written smaller, to distinguish it from the sum proper.

	T	U
	1	5
+		8
	2	3
	1

The one that is carried could also be put as a small number just by the one in the tens column, but that can be confusing, making the tens column look like 11 (ten plus one), rather than 1 plus one.

Here are examples adding three numbers together:

T U   2 1 +   6     5   3 2   1

T U   4 6 +   7   1 9   7 2   2

H T U     5 2 + 1 3 1     9 8   2 8 1   1 1

writing down subtraction sums

Again, although it is possible to write subtraction sums horizontally, 9-5=4, it is often more useful to write them in columns.

	9
-	3
	6

When the sum includes groups of more than ten items, say 17, a second (tens) column should be made.

	T	U
	1	7
-		5
	1	2

Complications start when the number in the units column being taken away is larger than the units from which it is being taken, for instance 11-8=3. 1 minus 8 gives a negative number, which does not exist in the real world.

	T	U
	1	1
-		8
		3

So what to do? I was taught to ‘borrow’ (transfer) one ten from the tens column, adding it to, in this case, the one in the units column. The one in the tens column is crossed out, and a small one is put just before the one in the units column. Then a subtraction can be done of eleven minus eight.

Thus the units column, in fact, now contains eleven units and the ‘one ten’ disappears (is crossed out) from the tens column. All that has happened is the ten has been moved across to another (the units) column.

	T	U
	1	11
-		8
		3

When the number in the tens column is greater than one, that number less ‘one ten’ is written small in the tens column and the ten is added to the units column.
So for the subtraction, 33-17=16:

	T	U
	32	13
-	1	7
	1	6

The analogous process will be continued with three columns, where a single hundred becomes ‘ten tens’ in the tens column. And so on where one thousand becomes ‘ten hundreds’ .

advertising disclaimer

writing down multiplication sums

You will recall that multiplication is the adding of a collection of objects several times. Multiplication sums are laid out as a sort of shorthand so, for instance, adding a collection of two objects together three times can be written as 2 x 3 = 6. In words, three lots of two objects added together makes six objects, or two times three equals six.

The sum can also be written as below:

	T	U
		2
x		3
		6

When the total of items added together is more than nine, they are made into a collection of ten items and any left over are kept in a collection of ‘units’. In the sum written out below, there are no units left over, as two times five makes ten, which is written as one ten and no units: 10.

	T	U
		5
x		2
	1	0
	1

The next multiplication sum is adding together two lots of 12: 12x2. Although the learner may have made a cross table up to twelve (we have only shown a cross-table up to ten) or may remember their two times table up to twelve (or their twelve times table), by laying the multiplication sum out as below, they will have a method that will work for any multiplication made with a collection smaller than ten.

	T	U
	1	2
x		2
	2	4

The answer for adding two collections of two goes below in the units column and, likewise, the one collection of ten times two goes in the tens column.

Where the continuous adding of collections smaller than ten - the units - results in a total greater than nine, the group of ten items is carried forward to the tens column, to be added to the result of the tens column multiplication.

	T	U
	1	4
x		3
	4	2
	1

‘Long multiplication’ or extended multiplication is similar to the simple multiplications above, but the multiplications for each part - units, tens.... - is calculated and recorded separately, then added together for a final answer.

Take, for example, the long multiplication of 83 times 27. This is broken into two parts:

• multiplying 83 with tens - two lots of ten (20), this sub-sum being 83x2 - and
• multiplying 83 with units - seven units (7), this sub-sum being 83x7.

These sub-sum results are then added together.

To write the multiplication with tens, in this case two tens (twenty), a holding digit - zero - is put in the units column. This holding digit ensures that the multiplication with tens is automatically placed in the correct columns for the final addiing up (addition).

Note that

• I have added more column headings, T for Thousands and H for Hundreds, to help keep the calculation organised
• carrying figures are included as needed;

	T	H	T	U
			8	3
x			2	7
	1	6	6	0	multiplication with two tens
		5	82	1	multplication with seven units
	2	2	4	1	addition of the two sub-sums
	1	1

Here is another long multiplication, this time multiplying 123 by 123. This one is broken into three parts:

• multiplying 123 with hundreds - one lot of one hundred (100), this sub-sum being 123x100 - and
• multiplying 123 with tens - two lots of ten (20), this sub-sum being 123x2 - and
• multiplying 123 with units - three units (3), this sub-sum being 123x7.

These sub-sum results are then added together.

To write the multiplication with hundreds, in this case one hundred (100), holding digits - zeroes - are put in the tens and the units columns.
To write the multiplication with tens, in this case two tens (twenty), a holding digit - zero - is put in the units column.
These marker digits ensure that the multiplication with hundreds or with tens are automatically placed in the correct columns for the final addiing up (addition).

		T	H	T	U
			1	2	3
x			1	2	3
	1	2	3	0	0	multiplication with one hundred
		2	4	6	0	multiplication with two tens
			3	6	9	multplication with three units
	1	5	1	2	9	addition of the three sub-sums
		1	1

writing down division sums

Writing down division sums is done somewhat differently from addition, subtraction and multiplication sums. Here, we will start by describing division into less than ten parts. Later, we will do some ‘long (but not very long) division’.

Division sums are often written in the ‘shorthand’ form of, say, 14÷2=7 (or 14/2=7). In this division sum, two is being constantly subtracted from fourteen - in fact, it is subtracted seven times. The notation ÷ or / can be described (or interpreted as) ‘constantly subtracted by’, or ‘divided by’.

Although for a relatively simple division sum, it is not necessary to lay out the division sum as done for dividing bigger numbers, it can be regarded as a good habit, as well as providing a consistent method. The more complicated the sum, the more it is helpful to write it so the steps in the division can be followed, and so much of the working is incorporated.

So, for writing down and providing clarity of working, 14÷2=7 is writtten thus:

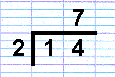
The number being divided is put inside the L-shape, the number doing the dividing is put on the left of the vertical line, and the answer is put above the horizontal line.

For larger sums, involving hundreds or even thousands, as well as tens and units, it is essential to hold in mind that each column, from left to right, holds ten times as many objects as the column to its immediate right - hundred is ten lots of ten, and ten is ten lots of units (one).

Thus, in the division sum below, three lots of a hundred, and five lots of ten, and two units are to be divided (or shared) into eight parts.

The next division sum is 352÷8. The working out the sum (calculation) in four steps is followed by an explanation, the numbers being used in the sum written in bold.

1. Three, being smaller than eight, cannot have eight subtracted from it even once
   (eight does not divide into three).

   With the three being a collection of ten times as many objects as the five to its right, the three and five together behave rather like thirty-five.

2. This ‘35’ is divided by eight, or
   eight is subtracted until there is nothing or less than eight left.
   In this case, eight can be subtracted four times (can be divided into 35 four times) with three left over - a remainder of three (in pink to distinguish it from the division sum as originally written).
   The answer of four is written above the horizontal line, in the tens column (the division was of 35 tens).
   
   
3. The remainder of three (remember that is three lots of ten) is added to the two units, being written as a small three just before the two.
   The last part of this division is three tens plus two units (32) divided by eight (or eight subtracted, in this case, four times).
   
   
4. The answer of four is written above the horizontal line, in the units column (the division was of 32 units).

Now this many seem rather a laborious explanation to those who have done division so many times, and who have properly learnt their times tables. For them, these steps now happen pretty well automatically (except perhaps remembering some of the times table and working out the reminder to carry forward). But for a beginner, it is a great help to be aided by explanations of each step that do not glide over a step so simple that it just assumed to be done without instruction.

The next division sum is 5293÷7. The working out the sum (calculation) is shown in four steps, the numbers carried being shown in pink.

The final sub-sum of 43÷7 gives a reminder of of one, or one left over. This is recorded at the end of the answer as r.1 - r. being an abbreviation of remainder.

calculation ‘shortcuts’

There a number of calculation ‘shortcuts’ to help with divisions. However, some are more useful than others, and some are practically no use at all, other than as an amusement and diversion. They should not be used as a sunstitute for understanding how division works, but regarded as possibly useful tools that may speed up a calculation.

• All numbers divisible by two end in an even number (2,4,6,8) or in zero (0).
• For all numbers divisible by three, the sum of the digits is also divisible by three, but that sum will be a much smaller, more recognisable number.
  For instance, 483 ‘adds up’ like this: 4+8+3=15, and 15 is divisible by three (15÷3=5), so 483 must be divisible by three.
  Here is a longer example, 123456789. The digits add 1+2+3+4+5+6+7+8+9=45. 4 and 5 make 9, so 123456789 can be divided by three.
• If the last two digits form a number divisible by four, then the complete number is divisible by four.
  Example: 569828. The last two digits are 28. 28÷4=7, therefore 569828 is divisible by four.
• All numbers ending in either five (5) or in zero (0) can be divided by five.
• Numbers divisible by six must be divisible by both two and three. That is, the last digit will be even or zero, and the number’s digits add up to three or a multiple of three.
• Determining whether a number is divisible by seven is a bit more complicated. There are several methods, but I shall just explain one method here.
  The idea is, double the last digit and subtract that doubling from the rest of the digits. If the result can be divided by seven, then so can the complete number.
  For example using the number 434, doubling 4 gives 8: 43-8=35. 35 is divisible by 7 (five times), so 434 is divisible by seven. Note that as the number being examined becomes larger, so this method become ever more laborious. Thus it can take nearly as much effort to check for divisibility as it does to do the division by seven.
• To see whether a number can be divided by eight, check its last three numbers.
  If the first number is even, the number is divisible by eight if the last two numbers are divisible by eight. So 648 can be divided by 8.
  If the first number is odd, subtract 4 from the last two numbers. If that result is divisible by eight, then the whole number will be as well. Thus, for 1352 subtract 4 from 52: 52-4=48. 48 can be divided by by 8, so 1352 is divisible by 8.
• A number is divisible by nine if the sum of its digits can be divided by nine. For example, the digits of the number 261 add up to nine (2+6+1=9). Thus 261 is dismissible by nine.
• All numbers ending in zero can be divided by ten.

writing down long division sums

Long division, dividing a number bigger than ten into another number, can be seen as doing several, consecutive, smaller division sums.

For larger sums, involving hundreds or even thousands, as well as tens and units, it is essential to hold in mind that each column, from left to right, holds ten times as many objects as the column to its immediate right - hundred is ten lots of ten, and ten is ten lots of units (one).

So a long division sum such as 952÷17, nine lots of hundred, and five lots of ten, and two units (or ones) are to be divided (or shared) into seventeen parts. The smaller, sub-sums are organised thus:

• the hundreds divided by seventeen,
• next the tens, plus any hundreds that are a reminder from the first sub-division sum, divided by seventeen,
• then the units, plus any tens that are a reminder from the second sub-division sum, divided by seventeen.

The number being divided is put inside the L-shape, the number doing the dividing is put on the left of the vertical line, and the answer is put above the horizontal line.

The working out the sum (calculation) in four steps below is followed by an explanation, the numbers being used in the sum written in bold.

1. 17 is too big to divide into 9, 17 does not ‘go into’ 9. Remember, you are seeing how many times 17 can be subtracted, in this case from 9.
   If it is helpful, you can put a zero above the nine, on the answer line, to show 17 ‘goes into’ 9 no times, but this zero will not be included in the final answer. (We have ‘written’ zero lightly to indicate that it is optional.)
2. The remainder - 9 - from the first sub-sum is put as its result. This is written similarly to the subtraction sums described above.
   Now we bring down the 5 tens to create the next number for the next sub-sum.
3. 17 ‘goes into’ 95 five times - you can subtract 17 from 95 five times.
   The 5 is written as part of the answer at the top of the division sum.
   The remainder - 10 - from this second sub-sum is put as its result.
4. Now we bring down the 2 units (ones) to create the next number for the next sub-sum. 17 can be subtracted six times from 102 - 17 ‘goes in’ 102 six times.
   The 6 is written as part of the answer at the top of the division sum.
   There is no reminder.

A bigger long division sum, say with thousands as well, or with a larger divisor, is performed in a similar fashion.

In doing long and complex calculations, some learners can take delight (and satisfaction) in doing the multiplications and subtractions needed to complete the sub-sums. Other learners may become frustrated or overwhelmed. It is normal for humans to make regular errors when transcribing in detailed calculations, just as you will find mis-spellings even in the most rigorously edited books.

“Let him [the abbot] so temper all things that the strong may have something to strive for and the weak have nothing to dismay them.”

“IF A BROTHER IS COMMANDED TO DO THE IMPOSSIBLE
If it happens that orders are given to a brother which are too heavy or impossible, let him receive the order of his superior with perfect gentleness and obedience. But if he finds that the weight of the burden is altogether beyond his strength to fulfil, then let him explain to his superior the reasons why he cannot do it, patiently at a suitable time, without showing any pride or resistance or contradiction. Then, after his representations, if the superior remains firm in requiring what he has ordered, let the subject realise that it is better so, and out of charity, trusting in the help of God, let him obey.”
[The rule of Saint Benedict for monasteries]

Good teaching is not simple.

writing down longer long division sums

As described just previously, long division sums, which involve dividing a number bigger than ten into another number, can be seen as doing several, consecutive, smaller division sums.

For these larger sums, it is essential to hold in mind that each column, from left to right, holds ten times as many objects as the column to its immediate right -

• hundred thousand is ten lots of ten thousand
• ten thousand is ten lots of a thousand
• thousand is ten lots of a hundred
• hundred is ten lots of ten
• and ten is ten lots of units (one).

So with a longer long division sum such as 987,654,321÷145,
nine lots of hundred million,
and eight lots of ten million,
and seven lots of a million,
and six lots of hundred thousand,
and five lots of ten thousand,
and four lots of thousand,
and three lots of hundred,
and two lots of ten,
and one unit (or one) are to be divided (or shared) into one hundred and forty-five parts.

The smaller, sub-sums are organised thus:

• the hundred millions divided by a hundred and forty-five,
• next the ten millions, plus any hundred millions that are a remainder from the first sub-division, divided by a hundred and forty-five
• then the millions, plus any ten millions that are a remainder from the second sub-division, divided by a hundred and forty-five
  In this long division sums, the first calculable sub-division, that is one that starts with a number greater than the divisor, 145, is the next sub-division.
• next the hundred thousands, plus any millions that are a remainder from the third (first calculable) sub-division, divided by a hundred and forty-five
• then the ten thousands, plus any hundred thousands that are a remainder from the fourth (second calculable)sub-division, divided by a hundred and forty-five
• next the thousands, plus any ten thousands that are a remainder from the fifth (third calculable) sub-division, divided by a hundred and forty-five
• then the hundreds, plus any thousands that are a remainder from the sixth (fourth calculable) sub-division, divided by a hundred and forty-five,
• next the tens, plus any hundreds that are a reminder from the seventh (fifth calculable) sub-division sum, are divided by a hundred and forty-five,
• lastly the units, plus any tens that are a reminder from the fourth (sixth calculable) sub-division sum, divided by a hundred and forty-five divided by seventeen.

The number being divided is put inside the L-shape, the number doing the dividing is put on the left of the vertical line, and the answer is put above the horizontal line.

The working out the sum (calculation) in six steps below is followed by an explanation, the numbers being used in the sum written in bold. Numbers carried forward as part of multiplications [going to the left] are shown in pink, while numbers borrowed as part of subtractions and taken to the next column [to the right] are shown in blue.

Here follows a worked example for the longer longer division sum 987,654,321÷145. I have ‘cheated’ a bit with the choice of divisor, so that the multiplications needed to caculate the necessary multiples of the divisor are not too time consuming. Of course, you can construct ever more interesting longer long division sums for yourself. How about 1,023,456,789÷777?

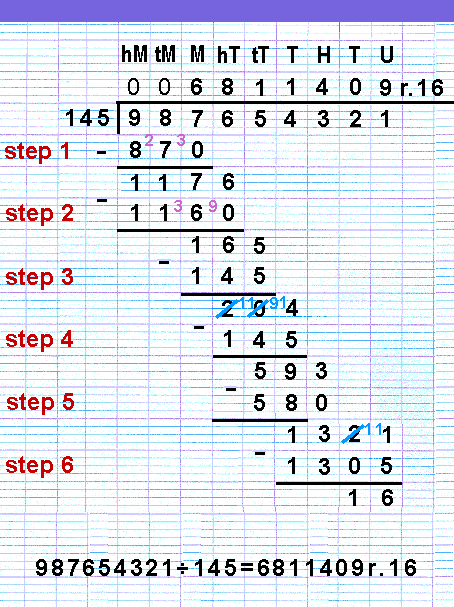
1. 145 is too big to go into either 9 or 98, 145 does not ‘go into’ either 9 or 98. Remember, you are seeing how many times 145 can be subtracted.
   If it is helpful, you can put a zero above the 9 and the 8, on the answer line, to show 145 ‘goes into’ 9 and into 98 no times, but these zeros will not be included in the final answer. (We have ‘written’ zero lightly to indicate that it is optional.)
   So, the first sub-division sum is 987÷145.
   145 ‘goes into’ 987 six times - you can subtract 145 from 987 six times.
   [Mental arithmetic tip: consider that 145 is 150-5. Two lots of 150 is 300, six lots of 150 is 900, and six lots of 145 will be less (six times 5 less) than 900. So 145 can be subtracted six times from 987.]
   The 6 is written as part of the answer at the top of the division sum.
   The remainder - 117 - from this first sub-sum is put as its result. This is written similarly to the subtraction sums described above.
   
2. Next we bring down the 6 hundred thousands to create the next number for the next sub-sum.
   145 ‘goes into’ 1176 eight times - you can subtract 145 from 1176 eight times.
   [Mental arithmetic tip: consider that 145 is 150-5. Two lots of 150 is 300, eight lots of 150 is 1200, and eight lots of 145 will be less (eight times 5 less) than 1200. So 145 can be subtracted eight times from 1176.]
   The 8 is written as part of the answer at the top of the division sum.
   The remainder - 16 - from this second sub-sum is put as its result.
   
   
3. Now we bring down the 5 ten thousands to create the next number for the next sub-sum.
   145 ‘goes into’ 165 once - you can subtract 145 from 165 one time.
   The 1 is written as part of the answer at the top of the division sum.
   The remainder - 20 - from this third sub-sum is put as its result.
   
   
4. Next we bring down the 4 thousands to create the next number for the next sub-sum.
   145 ‘goes into’ 204 once - you can subtract 145 from 204 one time.
   The 1 is written as part of the answer at the top of the division sum.
   The remainder - 59 - from this fourth sub-sum is put as its result.
   
   
5. Now we bring down the 3 hundreds to create the next number for the next sub-sum.
   145 ‘goes into’ 593 four times - you can subtract 145 from 593 four times.
   The 4 is written as part of the answer at the top of the division sum.
   The remainder - 13 - from this fifth sub-sum is put as its result.
   
   
6. Next we bring down the 2 tens to create the next number for the next sub-sum. But 145 is bigger than 132, so 145 can be subtracted from 132 no times - 145 goes into 132 no times. So a zero is written as part of the answer at the top of the division sum.
   We now bring down the 1 unit to create the number for the final sub-sum.
   145 can be subtracted nine times from 1321 - 145 ‘goes into’ 1321 nine times.
   [Mental arithmetic tip: consider that 145 is 150-5. Two lots of 150 is 300, nine lots of 150 is 1500, and nine lots of 145 will be less (nine times 5 less) than 1500. So 145 can be subtracted nine times from 1321.]
   9 is written as part of the answer at the top of the division sum.
   There is a reminder of 16.

end notes

1. Tom Lehrer, author of many sharp, if also hilarious, songs, wrote one on doing sums - New Math, involving the sum 342-173.
   
   New Math

   Introduction

   Some of you who have small children may have perhaps been put in the embarrassing position of being unable to do your child's arithmetic homework because of the current revolution in mathematics teaching known as the New Math. So as a public service here tonight I thought I would offer a brief lesson in the New Math. Tonight we're going to cover subtraction. This is the first room I've worked for a while that didn't have a blackboard so we will have to make due with more primitive visual aids, as they say in the "ed biz." Consider the following subtraction problem, which I will put up here: 342 - 173.

   Now remember how we used to do that. three from two is nine; carry the one, and if you're under 35 or went to a private school you say seven from three is six, but if you're over 35 and went to a public school you say eight from four is six; carry the one so we have 169, but in the new approach, as you know, the important thing is to understand what you're doing rather than to get the right answer. Here's how they do it now.

   You can't take three from two,
   Two is less than three,
   So you look at the four in the tens place.
   Now that's really four tens,
   So you make it three tens,
   Regroup, and you change a ten to ten ones,
   And you add them to the two and get twelve,
   And you take away three, that's nine.
   Is that clear?

   Now instead of four in the tens place
   You've got three,
   'Cause you added one,
   That is to say, ten, to the two,
   But you can't take seven from three,
   So you look in the hundreds place.

   From the three you then use one
   To make ten ones...
   (And you know why four plus minus one
   Plus ten is fourteen minus one?
   'Cause addition is commutative, right.)
   And so you have thirteen tens,
   And you take away seven,
   And that leaves five...

   Well, six actually.
   But the idea is the important thing.

   Now go back to the hundreds place,
   And you're left with two.
   And you take away one from two,
   And that leaves...?

   Everybody get one?
   Not bad for the first day!

   Hooray for new math,
   New-hoo-hoo-math,
   It won't do you a bit of good to review math.
   It's so simple,
   So very simple,
   That only a child can do it!
   Now that actually is not the answer that I had in mind, because the book that I
   got this problem out of wants you to do it in base eight. But don't panic. Base
   eight is just like base ten really - if you're missing two fingers. Shall we
   have a go at it? Hang on.

   You can't take three from two,
   Two is less than three,
   So you look at the four in the eights place.
   Now that's really four eights,
   So you make it three eights,
   Regroup, and you change an eight to eight ones,
   And you add them to the two,
   and you get one-two base eight,
   Which is ten base ten,
   And you take away three, that's seven.

   Now instead of four in the eights place
   You've got three,
   'Cause you added one,
   That is to say, eight, to the two,
   But you can't take seven from three,
   So you look at the sixty-fours.

   "Sixty-four? How did sixty-four get into it?" I hear you cry.
   Well, sixty-four is eight squared, don't you see?
   (Well, you ask a silly question, and you get a silly answer.)

   From the three you then use one
   To make eight ones,
   And you add those ones to the three,
   And you get one-three base eight,
   Or, in other words,
   In base ten you have eleven,
   And you take away seven,
   And seven from eleven is four.
   Now go back to the sixty-fours,
   And you're left with two,
   And you take away one from two,
   And that leaves...?

   Now, let's not always see the same hands.
   One, that's right!
   Whoever got one can stay after the show and clean the erasers.

   Hooray for new math,
   New-hoo-hoo-math,
   It won't do you a bit of good to review math.
   It's so simple,
   So very simple,
   That only a child can do it!

   Come back tomorrow night. We're gonna do fractions.
   Now I've often thought I'd like to write a mathematics text book someday because I have a title that I know will sell a million copies. I'm gonna call it Tropic Of Calculus.

   
   That Was the Year That Was by Tom Lehrer 1966, re-issued as CD in 1990; Wea/Warner Brothers; ASIN: B000002KO7
   $10.99 [amazon.com] {advert}/ £9.98 [amazon.co.uk] {advert}
   
   
   
   
   
   
   
2. Although for learners it not necessary, and may be confusing, teachers of mathematics may well use technical terms for things like ‘the number doing the dividing’, or ‘the number being multiplied’.
   
   So, for multiplication sums, multiplicand x multiplier = product; and
   for division sums, dividend ÷ divisor = quotient.
   
   
3. Benedict of Clairvaux (1090 – 20 August 1153) The rule of Saint Benedict for monasteries, a translation by Dom Bernard Basil Bolton OSB, monk of Ealing Abbey, 1968.

email email_abelard [at] abelard.org

© abelard, 2009, x july

all rights reserved

the web address for this page is https://www.abelard.org/sums/teaching_number_arithmetic_mathematics_writing_down_sums.php

4430 words
prints as 12 A4 pages (on my printer and set-up)