introducing simultaneous equations
Before starting to study this page, first make sure that you have read as far as you need of
equality and equations - keeping sums in balance, depending on how much you understand about equations.
Working with simultaneous equations is a matter of working with more than one equation at a time [simultaneously], and with more than one variable in the equations.
While this page will deal with calculations involving two equations and variables, keep in mind the extension of these techniques can be applied to three, four, five equations with three four, five variables, and upwards.
These things are not difficult, but merely complicated, thus making it necessary for you to work carefully and systematically, do not panic, or run in circles screaming and shouting.
As resolving [finding the answers to] simultaneous equations is complicated, careful and tidy layout is important to avoid confusion, or becoming lost in a tangled web of spidering ink blot.
Graphs are idealised curves or lines, the real world tends to be knobbly and awkward.
Here is an example question,
"What are the two numbers which added together total -33, and which have a difference of -117 ?"
But there's no need to be stumped, there's a rather smart and relatively easy way of answering such a question - using simultaneous
equations!
With simultaneous equations you find the values of the two
unknown variables, using two equations that describe the question.
This is how you turn the question into two equations:
For this example, the equations are
"two numbers which added together total -33",
or x + y = -33
and "which have a difference of -117",
or x - y = - 117
In this page we will describe how to use and resolve simultaneous equations.
(Here is shown a fully worked answer for the question above.) |
about simultaneous equations
Simultaneous equations are solved by using a combination
of ‘methods’ or techniques. Frequently, these
methods are described as if they are discretely different,
but often the methods are very similar. This has been described
to me as choosing to describe travelling along a road either
as taking a journey, or as going from A to B. Both descriptions
describe the action of travelling, but in different ways.
- The main methods for solving simultaneous equations can be broken down into several methods such as :
- elimination,
substitution
and
drawing a graph (graphical method).
- For instance, the GCSE curriculum specifies two methods, or techniques, for solving simultaneous equations.
- • One method is to multiply both equations by constants so one unknown becomes the
same in both equations; then add the equations or subtract one equation from the other, to eliminate one unknown.
• Another method is to express one unknown in terms of the other by rearranging
(transforming) one equation - see equality and equations;
the expression thus obtained is substituted into the other equation.
There can be confusion because the word substitution may be used to describe two actions:- • when the value found by addition/subtraction is inserted into one equation
to find the second value. (There are numerous examples below, such as here and here). However, here the word ‘substitute’
is frequently used rather than ‘insert’.
This can lead to some confusion.
• when, having expressed one variable in terms of the
other using one equation, that expression is substituted
into the other equation (see the second GCSE method below).
- These two actions are pretty similar, the difference
being substituting a single variable’s value, or
substituting an expression made up of several variables.
Which technique or techniques are used depend on the
problem presented. However, drawing a graph may done with
any equation.

As with the introductory example above, simultaneous equations often are presented, not as a
pair of equations, but as a written description of the
problem to be solved. We will look at other examples of this later on.

Finally, remember that when there are two variables to
be found, say x and y,
necessarily this is a two-stage operation, with a stage
for finding the value of each variable.
Note: The different methods such as elimination and substitution,
subtraction, addition, division, or multiplication are referred to and used in several sections on this page.
However, the occurrences are illustrating different
steps in the solving of different simultaneous equations. Thus
the apparent repetition has a purpose, defined by the stage
that has been reached in the particular calculation and the order
in which different methods have been chosen to be used.
Examining simultaneous equations
Before solving a pair of equations, you will need
to examine them and make a mental plan of action in order to choose which method or methods to use
for solving them.
You could find that you choose to use elimination
to find one variable, and substitution
to find the other.
- Look at whether one variable is the same in both equations, as for example, in this pair of simultaneous equations:
Here
as a first stage, by subtracting one equation from the other,
the variable 2y can be eliminated
(2y - 2y = 0 or nothing) and the value of x found.
- For the following pair of equations, two variables have the same value (2) but different signs (+/-).
x + 2y = 7 (i)
3x - 2y = -3 (ii)
By adding the two equations together, the variable 2y can be eliminated
[(+2y) + (-2y) = 0 or nothing] and again, the value of x found.
Elimination
- Here, one variable (either x or y) is eliminated
- by adding the two equations together, or
by subtracting one from the other.
- This will give the value of one variable which is the inserted (substituted) into one of the equations to find the value of the other variable.
-
- For example,
- 2x + 3y = 9 (i)
3x - 3y = 6 (ii)
Adding (i) and (ii) eliminates the variable
y- 2x + 3x + 3y -3y = 9 + 6
5x = 15
x = 3
The resulting equation has only one unknown, in
this case y, that then
can be solved.
- Substituting x = 3 into (i),
- 6 + 3y = 9
3y = 9 - 6
3y = 3
y = 1
Always back-check the result, in this case, for example,
by substituting y = 1 into equation (ii)- (3 x 3) - (3 x 1) = 6
Therefore, x = 3, y= 1 (ans.) |
|
advertising disclaimer
|
If there is no obvious addition or subtraction apparent,
then one or both of the equations may be first altered
by multiplication or division, so that one equation can
then be added, or subtracted, from the other.
- Consider the following equations
- 3x + 2y = 4 (i)
2x - y = 5 (ii)
Neither of the terms x or y can be eliminated
by adding or subtracting.
- Multiplying (ii) by 2, gives
- 4x -2y = 10 (iii)
Adding (i) and (iii) eliminates 2y- (3x + 2y) + (4x - 2y) = 4 + 10
- 7x = 14
x = 2
-
- Substitute 2 for x into
either of the original equations to find the value
for y.
- 3x + 2y = 4 (i)
6 + 2y = 4
2y = 4 - 6
2y = -2
y = -1
-
- Back-check using (ii),
- (2 x 2) - (-1) = 5
-
- Therefore x = 2, y = -1 (ans.)

Here is another example where both equations are first manipulated by multiplication:
3x + 4y = 32 (i)
2x - 3y = -7 (ii)
By multiplying (i) by 2 and (ii) by 3, the
variable x will have the
same value in the two resulting equations.
2(3x + 4y = 32)
6x + 12y = 36 (iii)
3(2x - 3y = -7)
6x - 9y = -21 (iv)
Subtracting equation (iv) from equation (iii) will eliminate the variable x and allow the value of y to be found.
12y - (-9y) = (64-(-21))
17y =
85
y = 5
Substituting y = 5 into (iv) to find the value of x:
6x - 45 = -21
6x = -21 - (- 45)
=
24
x = 4
- Checking using (i),
- (3 x 4) + (4 x5) = 32
12 + 20 = 32
-
-
- Therefore x = 4, y = 5 (ans.)
|
Substitution
This is a more generalised method of resolving simultaneous equations. It is abelard's preferred method.
The substitute method is also the preferred option for
solving a pair of equations where one contains x²,
y², or xy.
First a simple example,
x + y = 5 (i)
2x + 3y = 7 (ii)
Here, one of the variables, in this case x,
is isolated (put by itself) using equation (i)
x = 5 - y (iii) [ y has been subtracted from both sides of equation (i) ]
- Substitute (iii) into (ii)
- 2(5 - y) + 3y = 7
10 -2y + 3y = 7
10 - y = 7
-y = 3
y = -3
-
- Substituting y = -3 into (i),
- x = 5 - (-3)
x = 8
-
Checking using (ii),- (2 x 8) + (3 x (-3)) = 7
- x =8, y = -3 (ans.)
|
Thus, one equation is transformed into x = (something), or
y = (something). Then this something is substituted into
the other equation.
Now an example which contains x², y², or xy. There will be two values for each squared number (x², y²).
x2 + y2 = 5 (i)
y = 3x+1 (ii)
Substitute in the value of y from (ii) into (i).
x2 + (3x+1)2 = 5
Expanding this:
x2 + 9x2 + 6x + 1 = 5
Consolidating (adding x2 and 9x2 so there is one x2 value) :
10x2 + 6x - 4 = 0
Put the equation into brackets :
(When this is not possible, the equation can be solved as a quadratic equation.)
(5x-2)(2x+2) = 0
Thus, x1 = 2/5 and x2 = -1
Now substitute these values into (ii), to find two corresponding values of y.
when x = 2/5,
y = 3(2/5) + 1
y = 11/5
when x = -1,
y = 3(-1) + 1
y = -2
x1 = 2/5, y1 = 11/5, x2= -1, y2 = -2 (ans.)
Where the answer is required as co-ordinates, these would be (2/5, 11/5) and/or (-1, -2). |
Drawing a graph
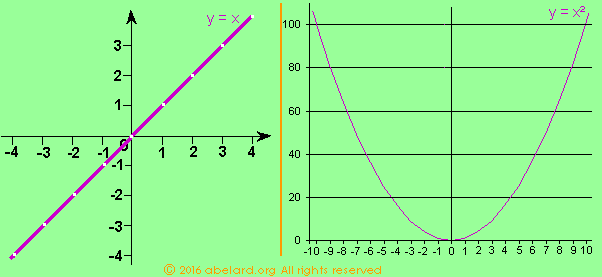
A two-dimensional graph has two axes, x and y (see graphs above),
while a three-dimensional graph has x, y and z axes.
This leads to the start of Cartesian algebra
, first developed by René Descartes in 17th-century France.
Cartesian algebra (also called the Cartesian co-ordinate system) can be used to describe a graph mathematically. Thus, Cartesian equations are a type of algebraic equation that involve the coordinates of the points lying on the graph/line.
- When x = y, the resulting line is at 45° [see left-hand graph above];
when x = y + 2, the line is displaced by 2 units.
- In practice, before drawing up the graph, start by isolating y on one side of the equation.
- The graphs of linear equations give straight lines.
- For equations that include x2, there are two crossing points, two solutions. The graph is a parabola [see right-hand graph above].
- Solving a simultaneous equation by drawing a graph is not difficult.
You draw the lines for each equation.
Then the point or points where the lines cross (their intersection/s) gives the solution.
The point/s can also be determined by calculation with simultaneous equations.
Example of solving simultaneous equations by drawing a graph
Now let's consider a graph with two straight lines, as might depict a pair of simultaneous equations.
It must be remembered that the solution to calculating a simultaneous equation
is the crossing point
of the two lines illustrating the two equations.
The calculation of a pair of simultaneous equations is not something airy-fairy and
magic, where you put numbers into a box called a formula or process, wind the handle by doing sums, and out pop answers of 'magic' and meaningless numbers.
Understand the what the steps of a calculation signify, and then the esoteric magic becomes a sum that makes sense.
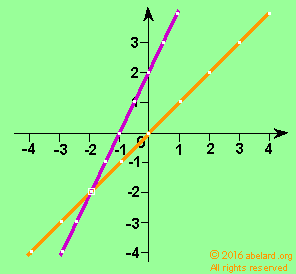 The answers can be calculated,
or by illustrated by a graph, a visual depiction of the calculation. The answers can be calculated,
or by illustrated by a graph, a visual depiction of the calculation.
The graph to the right is composed of
y = x (i)
y = 2x +2(ii)
Substituting (i) into (ii),
y
= 2y + 2
y - 2y = 2
- y = 2
y = -2 (iii)
Substituting (iii) into (i)
x = -2
x=-2, y = -2 (ans)
Looking at the graph, you can see this is where the two lines cross, that is where the two lines go through the same point and the lines (equations) become
simultaneous!
Yippee! |
- When both the graphs are lines (linear), then it is generally quicker to find the answer by algebra, unless you are being asked to find the answer using graphs.

The general form of a linear equation is y = mx + c. These equations in specific forms, as seen above, can be expressed (or illustrated) as a straight line on a graph using the methods of Descartes.
c is the value where the line cuts (goes across) the y axis of the graph. It is also known as the y Intercept.
A more basic linear equation is y = mx. Here, the line cuts the y axis at zero - see the orange line in the graph above.
Where the line crosses the axis can be manipulated, or altered, by dividing both sides by x.
 (If you don't understand how this works, go to how to teach your child number arithmetic mathematics - equality and equations.)
(If you don't understand how this works, go to how to teach your child number arithmetic mathematics - equality and equations.)
Using the equation y = mx, and isolating m
m = y / x
This is the equation for the angle of the sloping line, where m describes the slope, or gradient, of the line and is expressed as a fraction.
This angle is called the gradient of slope.
It's a bit like cycling up or down a hill. For example, if the length to be cycled is 100 yards or metres or … take your choice,
and you rise 15 metres on your track,
then the gradient is 15 metres over 100 metres.
x = 100 m, y = 15 m
m = 15/100
= 15%
That is damned steep - try it on a bike! A flight of stairs or a ladder can be much more steep.
Unless the steepness of the slopes (m) is the
same, whence the two lines are parallel, then at some point the two lines will cross. Whence there is common point that is on both lines. We can find this point out by calculation (see Example of solving a simultaneous equation by drawing a graph above).
written problems
Written problems have to be converted into equations so that the problem can be solved mathematically.
The first step is to determine the two values to be found and decide which variable will be x and which will be y.
Sometimes the question has done this already, as in the first example below.
Then two equations are generated that can be solved using simultaneous equation methods.
From GCE Summer 1971, Paper II, no. 9, optional.
For a school play, 300 tickets are sold. The cost per
adult was 55p and per child was 35p. It was later calculated
that if 60p had been charged for an adult and 30p for
a child, the total money would have been £9.00 more.
Letting x be the number of adults attending and y the
number of children, form two equations in x and y.
Solve the equations
to find the values of x and y.
Hence find the total amount
received from ticket sales. [Summer 1970, Specimen Paper, No.3, oblig.]
Answer:
x + y = 300 (i) [a total of 300 tickets had been sold]
55x + 35y + 900 = 60x +30y [money is in pence]
60x + 30y = 55x + 35y + 900
(60x-55x) + (30y -35y) = 900
5x+ (-5y) = 900
Dividing both sides by 5,
x - y = 180 (ii)
Add (i) + (ii)
2x = 480
x = 240
Substituting x = 240 into (i),
240 + y = 300
y = (300 - 240)
= 60
Thus 240 adults and 60 children attended.
(240 x 55p) + (60 x 35p) = £153.00
The total amount
received from ticket sales was £153.00 (ans.) |
James bought 2 bottles of lemonade and 1 bag of crisps for £1.40.
Jill bought 1 bottle of lemonade and 3 bags of crisps for £1.70.
How much is a bottle of lemonade? How much is a bag of crisps?
Answer:
Let a bottle of lemonade be x pence, a bag of crisps be y pence.
2x + y = 140 (i)
x + 3y = 170 (ii)
Re-arranging (ii),
x = 170 - 3y (iii)
Substituting (iii) into (i)
2(170 - 3y) + y = 140 (iv)
340 - 5y = 140
340 - 140 = 5y
200 = 5y
y = 40 (iv)
Substituting (iv) into (ii)
x + 120 = 170
x = 50
A bag of crisps cost 40p, a bottle of lemonade cost 50p (ans.) |
Alan has more money than Bertie. If Alan gave Bertie $20, they would have the same amount.
On the other hand, if Bertie gave Alan $22, Alan would then have twice as much as Bertie.
How much does each one actually have?
Answer:
Alan has x dollars, Bertie has y dollars.
x - 20 = y + 20 (i)
x + 22 = 2 (y - 22) (ii)
Re-arranging (i),
x = y + 40 (iii)
Substituting (iii) into (ii),
y + 40 + 22 = 2y - 44
- y = - 44 - 62
= -106
y = 106 (iv)
Substituting (iv) into (iii),
x = 106 + 40
= 146
Alan has $146, while Bertie has $106 (ans.) |
"What are the two numbers which added together total -33, and which have a difference of -117 ?"
In the question above, the two variables are the two numbers. I'll label them by x and y.
Now to work out x and y using two equations involving
these variables.
These equations are the simultaneous equations, 'simultaneous' because they are both used as part of the same calculating process.
Finding the solution for one equation enables finding the solution for the other equation.
(In sloppy parlance, they are solved “at the same time”.)
Always remember that the solution requires finding the values of both unknowns.
For this example, the equations are
"two numbers which added together total -33",
or x + y = -33 (i)
and "which have a difference of -117",
or x - y = - 117 (ii)
Note the two equations are numbered here so they can be referred to efficiently. (A different numbering is used so not to confuse with the 1,2,3 etc of the
actual values/numbers, or the x,y etc of the variables.)
- Looking at the two equations, you will see that there is + y and - y.
If added together, they cancel each other out, or their sum is zero, 0.
So adding together (i) and (ii),
2x + (y - y) = -33 + (-117)
This simplifies to- 2x = - 150
x = - 75
Next the value found for x is substituted into one of our original equations [equation (i)] :- -75 + y = -33
y = (75 -33)
y = 42
-
- Now check both answers by substituting both results into the other original equation [equation (ii)] :
- -75 - 42 = - 117
x = -75
y = 42 (ans.) |
this section is under development
linear programming
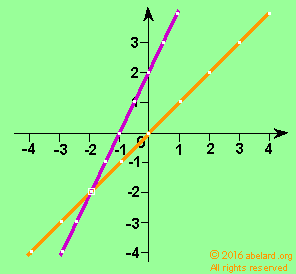 |
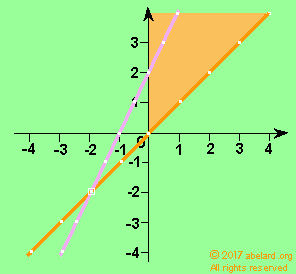 |
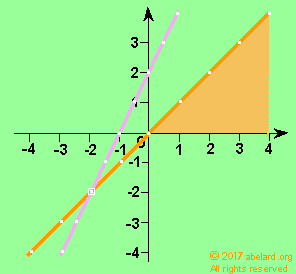 |
| equation |
greater than inequality |
less than inequality |
y = x (orange line)
y = 2x + 2 (purple line) |
using only y = x ( the orange line)
as a constraint |
using only y = x ( the orange line)
as a constraint |
These two equations, y = x and y = 2x + 2, are called equalities. That is, the left side of the equation is deemed equal to the right-hand side (rhs). But maybe you will be interested in what goes on above the line or below the line, whence the equations will change as follows:
- Taking the equation for the orange line
y = x above the line, that is where y is larger than x, the equation becomes y greater than or equal to x (≥ or >=).
If you are interested in where y is less than x, the equation will become y is less than or equal to x ( ≤ or <=).
When the connective is greater than (>) or less than (<), then the formulae are called inequalities.
- In the real world, most variables will be positive.
Such variables/values are plotted in the top right-hand quadrant (quarter, section) of a graph. Often, only this quadrant of a graph is shown.
Here are some examples:
• how much protein or calories it is reasonable to consume in a day,
• the number of workers in a factory,
• the hours available in a day or a year,
• or how much it will cost you to produce a bottle and the orange juice inside it.
Therefore, most of the equations or inequalities that will interest you in linear programming will fall into the top right quadrant of the graph.
And why would someone want to use linear equations?
Typical problems a manager may want to investigate are minimising costs or maximising output or profits.

making life complicated - trust me, i'm a scientist
"The diet problem was one of the first optimization problems studied
in the 1930s and 1940s. The problem was motivated by the Army's desire
to minimize the cost of feeding GIs in the field while still providing
a healthy diet. One of the early researchers to study the problem was
George Stigler, who made an educated guess of an optimal solution using a heuristic method. His guess for the cost of an optimal diet
was $39.93 per year (1939 prices). In the fall of 1947, Jack Laderman
of the Mathematical Tables Project of the National Bureau of Standards
used the newly developed simplex method to solve Stigler's model. As
the first "large scale" computation in optimization, the linear
program consisted of nine equations in 77 unknowns. It took nine
clerks using hand-operated desk calculators 120 man days to solve for
the optimal solution of $39.69. Stigler's guess was off by only $0.24
per year!"
Of course, for a million men that would save $1/4 million 1939 dollars
a year, or $10 or $20 million in today's deteriorated money, and would take at least 10 seconds to print.
Nowadays, large corporations run models with thousands of unknowns and thousands of variables, which are run daily or even hourly. These calculations can improve the company's profitability/efficiency by hundreds of millions of dollars each year. An example for Delta Airlines is quoted here.

There are copious resources on the internet and in books that will explain linear programming in incredible detail. As you see in the quotation above, with the advent of computer, linear programming has become a field for heavy-weight computer resources and number-grinding. This article, On linear programming, gives a useful introduction and will show you how to access widely available software such as Excel Solver.

You will notice that in linear equations, you can have hundreds of equations (or constraints). So instead of referring to variables by the likes of x, y and z, you will find the variable labelled as, for example, x1, x2, x3 etc as an easier notation. This does not change the meaning or intent of the algebraic descriptions (equations).
So the two expressions given above might become x1 = y1 and x2 = y2 + 2.
Remember that this is just a labelling system. There is no significance in which letters are used.
to be developed
Linear regression and correlation.
end notes
- Although this page, for
the most part discusses finding solutions for two variables
using simultaneous equations, it is possible to find
more than two variables. For instance, when solving
simultaneous equations by drawing graphs, a graph with
two axes will provide solutions for two variables, while
a graph with three axes, a three-dimensional graph,
will provide solutions for three variables.
- GCSE
- General Certificate of Secondary Education, academic
examinations taken at between 14 to 16 years old
in England, Wales and Northern Ireland, succeeding
the GCE, General Certificate of Education.
- Simple model answer:
- 2x + 3y = 9 (i)
3x - 3y = 6 (ii)
Adding (i) and (ii)- 2x + 3x + 3y -3y = 9 + 6
5x = 15
x = 3
- Substituting x = 3 into (i),
- 6 + 3y = 9
3y = 9 - 6
3y = 3
y = 1
Checking
by substituting y = 1 into equation (ii)- (3 x 3) - (3 x 1) = 6
Therefore, x = 3, y= 1 (ans.)
- The notation (how this equation is written) for y = mx + c
differs depending on the country you are in:
| In the UK, Australia, Bahamas, Bangladesh, Belgium, Brunei, Bulgaria, Cyprus, Egypt, Germany, Ghana, India, Indonesia, Ireland, Jamaica, Kenya, Kuwait, Malaysia, Malawi, Malta, Nepal, New Zealand, Nigeria, Oman, Pakistan, Peru, Poland, Singapore, Solomon Islands, South Africa, Sri Lanka, Turkey, UAE, Zambia and Zimbabwe |
y = mx + c |
| In the US, Australia again, Canada, Eritrea, Iran, Mexico, Portugal, Philippines and Saudi Arabia the notation is: |
y = mx + b |
| In Afghanistan, Albania, Algeria, Brazil, China, Czech Republic, Denmark, Ethiopia, France, Lebanon, Netherlands, Kosovo, Kyrgyzstan, Norway, Romania, South Korea, Spain, Tunisia and Viet Nam: |
y = ax + b |
| In Azerbaijan, China, Finland, Russia and Ukraine: |
y = kx + b |
| In Greece: |
ψ = αχ + β |
| In Italy: |
y = mx + q |
| In Japan: |
y = mx + d |
| In Cuba and Israel: |
y = mx + n |
| In Romania: |
y = gA + C |
| In Latvia and Sweden: |
y = kx + m |
| In Serbia and Slovenia: |
y = kx + n |
| [thanks to Rod Pierce] |
|
- The Latinised form of the name, Descartes, is Cartesius. It is from this word that the adjective Cartesian is derived.
|



















