site map

sums will set you free

how to teach your child numbers arithmetic mathematics

understanding sets and set logic

While set logic can be useful in thinking about problems, it is easy to become confused. Set logic was primarily only developed in the nineteenth century, and introduced in about 1960 into schools, when it was amusingly referred to as modern maths. It is very common that it takes a long time for knowledge to filter down from the inventors and discoverers (note).

Set logic is particularly difficult in that those who developed it were often slightly barmy and often very confused.

In language, very similar things can be said in more than one way. For example, I can refer to my house, while another person may refer to “that house over there in the forest”. Thus, in mathematical terms, someone might choose to say

“that house over there in the forest” = “my house”, or
“that house over there in the forest” equals “my house”, or
“that house over there in the forest” is the same as “my house” .

Similarly, you may say “seventy kilograms equals eleven stones”.

Sets, or set logic, is just another way of describing the real world, or even an unreal world if you are somewhat semi-detached! But don’t confuse the young with this, much better to teach them chess and let them have some fun absorbing and understanding a bunch of mad make-up rules, or let them read Alice through the looking glass.

It has been the hope or vanity that any object, quality or proposition can be substituted for the variables, and you will end up with ‘logical’ results. This is a false hope. In fact, it is widely used to put a ‘scientific’ veneer on confusion and nonsense. It was developed often with the ambition of ‘logicising’ mathematics and, thereby, somehow putting it beyond dispute. I shall be adding a short bibliography to this section should you wish to dive in and consume copious quantities of your own time.

invention and discovery

You can invent fairies at the bottom of your garden, but you can discover grass. Mathematics (and language) is an invention, and that invention is useful for describing the real world. But the language, although it exists in the real world, is not the real world which you are trying to describe. This has often confused people mightily. The map of the road is not the road, for a start you can’t drive on it, not for long anyway.

The word apple is not the real object apple. You may want a red, crunchy apple, but that remains one apple. The redness and the crunchiness are only qualities of the apple. Without the apple, the is no redness, nor crunchiness. Now the redness and the crunchiness are referred to as properties of the apple. But both are dependant on the existence of the real-world apple. Without understanding these things clearly, you will not understand set logic well. These problems, reality and the model, have often confused some some of the most creative modern mathematicians, let alone school teachers and their pupils.

If you do not have them clear in your own mind, you will sure as god made little red apples, confuse the learners.

It is important to concentrate on the fact that each apple is individual, and that it can only exist in one place at one time.

It does exist at any time (egg baskets). Of course, the apple can also be cut in half, or can be chewed up, at which time it becomes different or dispersed.

Most certainly, the apple cannot be ‘in’ two baskets ‘in’ the same sense, at the same time. For more discussion and examples.

As any property is dependant on an object, and the property goes along with the object, the property cannot be in two baskets at the same time.

zero

Zero (nought, naught, nil, null, nothing, nowt) usually written as 0, looks so innocent; but if taught sloppily or incorrectly, zero becomes the foundation for much difficulty and confusion.

Zero (0) has two main uses:

• As a placeholder, as in a thermometer; and
• to indicate nothing.

But there ain’t no such thing as nothing (see also Counting and addition). You can have an empty basket, or a basket without any eggs in it, or with no fairies in it, or even without a bath full of water in the basket. Of course, there is probably air in and around the basket, and there might be some dust, but in all circumstances, the basket remains whether empty or full of Easter eggs.

open and closed sets

Another confusion widely spread is the misuse of the operator “all”. This is often written as an upside down capital A: . You may talk (or write) of “all the apples in the basket”, but you cannot write reliably of “all the apples”. The basket and the apples within it comprise a closed set, whereas “all the apples” is an open set, unless you believe you are up to going around the planet counting all the apples, deciding what is and what is not an apple and making sure not to forget all the apples on the third planet from Beetlejuice. To attempt to apply set logic to open sets leaves you vulnerable to falling through the ice. I shall be discussing here set logic in the context of closed sets. See also the error of ‘infinity’.

category - logic blocks

Here is a list of words meaning category:
category, universal, predicate, property, class, set, attribute, type, collection.

The purpose of this section is to encourage and develop an understanding of the formation of collections. It will be soon needed in the next stage (multiplication). If you do not have logic blocks (yet?), onions and stones and insects and flowers and boxes of detergent will serve.

Logic blocks, also known as attribute blocks, are made as a set of plastic shapes. This is a four attribute set - shape, size, thickness and colour. The blocks can be sorted into groups of a specific attribute or several attributes.

what is a set?

It seems for many that it is remarkably easy to confuse a set for the contents of a set (what is ‘in’ the set). You can add apples to apples, or eggs to eggs, but the apples and eggs are always somewhere - in a basket, or on a table, or inside a chalk circle, or even as an idea inside your physical head.

A set can be spoken of as a collection, but who collected it and where?

Are you adding together the sets (boxes) with the objects, or are you adding them together in Startrek hyperspace or fairyland?

This becomes particularly dubious when people talk of adding ‘the null set’. What they usually mean is adding nothing/no thing - there is no set involved. If you add two baskets of eggs together, do you end up with the baskets as well as the eggs, or do you just end up with the eggs, and where have you put the eggs - make sure that they do not roll of the shelf, or you have not put them on the floor where you may step on them.

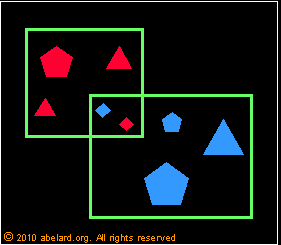It is a widespread confusion to believe that an object may be in two sets at the same time. This confusion can easily be reinforced by the use of Venn diagrams. The last three diagrams above are examples of Venn diagrams where a chalk or pencil line, or even an imagination in your real head, is deemed to represent a set. For example in the fourth diagram above, the red circles are supposed as being in both the set of circles and in the set of red items.

But it is vital never to start believing that the red circles are duplicated. The two red circles shown in the diagram remain only two blocks. By referring to the conjunction (AND) area in the diagram, you are in fact treating that area as a separate set, thus moving from two sets to three sets, you are thence forming a third set. Be very cautious to avoid this confusion from creeping into a learner’s belief system.

A block may be red and it may be round, but it is one, and only one, block. Properties are not objects. Without an object, there is no property beyond the imagination of a property within your own head.

Neither do you have any fully reliable certainty of just what the imagination is within someone else’s head. The best you can manage, or hope for, is to point at objects outside yourself with your finger, or big toe, in order to communicate as best as possible what you mean to another person, and likewise them to you.

logical operators/connectives - NOT, AND, OR, XOR

It is a manner of simplicity and mechanics that computers operate, essentially, with switches, which are set to ‘on’ or ‘off’. These are often interpreted as ‘on’ or ‘off’, or ‘yes’ or ‘no’, or ‘true ’ or ‘false’, or 1 or 0. [See also bases, when we reach it.] You can, of course, decide that ‘yes’ is apples and ‘no’ is oranges, or any other binary/bifurcation that suits you.

Just to make things awkward, various writers and teachers seem to delight in using, or inventing, an almost endless variety of symbols to express some very simple, basic ideas.

Most thoughtful seriously numerate people can do a great deal using the four basic operations of NOT, AND, OR and XOR (exclusive OR).

These basic operations are the foundation of set logic. It is important to make these foundations secure and rational. It is vital that understandings are founded securely in the real world at every step. A very great deal of maths teaching is not founded in this manner and is taught in vague and even incorrect abstractions. [Compare this area with teaching number - arithmetic - mathematics: introduction.]

The baskets can be represented by circles, at which point in order to be important or awkward, people often start referring to Venn diagrams.

NOT

NOT is a reversing, or negating, operator. Thus, NOT turns ‘yes’ to ‘no’, or ‘no’ to ‘yes’, or 1 to 0, or 0 to 1. NOT is sometimes called complement.

an apple	NOT an apple

Instead of ‘state’, you will often see a variable such as ‘p’ and ‘not p’ (or ~p). The idea being that ‘p’ is a variable and can be replaced by absolutely anything. The only problem is, this does nor work in the real world. That is, you cannot reverse anything, but this becomes too complicated to discuss here. If you care enough, you can go very deep diving in The confusions of Gödel. For the meanwhile, just keep to closed sets and simple cases such as either “an apple” or “not an apple”, or 1 and 0. Even true and false can be confusing. Remember, here I am just concerned with basics and, primarily, computer logic.

AND

This is called conjunction.

AND truth tables ( &   •   )
state	state	combined state		state	state	and state		state	state	and state
round	red	round red		True [T]	True [T]	True [T]		1	1	1
round	NOT red	round NOT red		True [T]	False [F]	False [F]		1	0	0
NOT round	red	NOT round red		False [F]	True [T]	False [F]		0	1	0
NOT round	NOT red	NOT round NOT red		False [F]	False [F]	False [F]		0	0	0

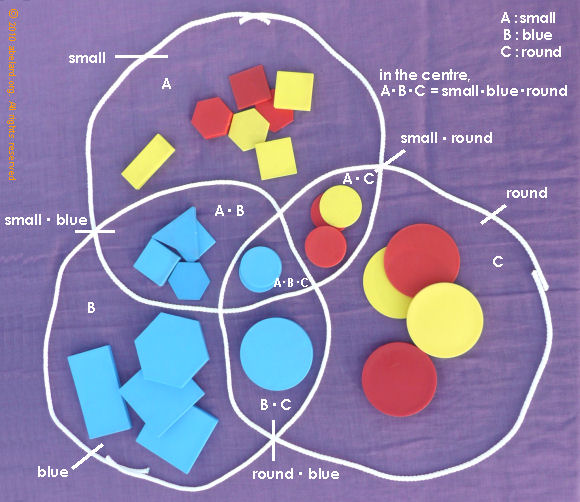
As you see, round and red [round^red] is the part in the middle of the photo above, where the blocks are both round and red. If the condition round and red is set up in a computer program, when testing for that condition, the result will be 1 (that is, true) only where both conditions are satisfied.

If either or both conditions are zero (NOT true), then the condition (that is, the AND conditon) is NOT true; or put otherwise, the condition fails. False is indicated by 0.

In the photo above, 0 0 [on bottom line of truth table] are the areas outside the circles but still on the table. The table top (purple) is the closed area being discussed. This is sometimes called “the universe of discourse” - that is, what we are talking about. However, we are concentrating on discussing the contents of the pencil-drawn circles, not the penknife or the pencil or its shavings. The gondaliers of Venice are also outside the area of discussion, as is my pet unicorn.

OR (inclusive OR)

An inclusive OR, that is: if either or both sets fulfill a condition, then the conjunction of the conditions comes out as true. When neither set fulfils this condition, then the condition comes out false. OR is called disjunction.

In all logical operators, in all cases, in among all the jargon, even terms like and and or are defined categorically by the truth tables. Any verbal description, or shorthand sign, is secondary.

OR (inclusive OR) truth tables (v   )
state	state	combined state		state	state	or state		state	state	or state
round	red	round red		True [T]	True [T]	True [T]		1	1	1
round	red	round NOT red		True [T]	False [F]	True [T]		1	0	1
NOT round	red	NOT round red		False [F]	True [T]	True [T]		0	1	1
NOT round	NOT red	NOT round NOT red		False [F]	False [F]	False [F]		0	0	0

XOR (exclusive OR)

An exclusive OR occurs only when either (only one) set fulfills a condition, the conjunction and the disjunction of the conditions being false.

connective/operator symbols

You will find that the signs for the connectives vary from book to book (or source to source). I have already introduced NOT, AND, OR and exclusive OR, you will find several signs and names being used to represent these, and other, operators.

NOT (also sometimes called complement)   ~   ¬
AND (also called conjunction)   &   •  
inclusive OR (also called inclusive disjunction)   v  

For example, you may find AND referred to as an intersection. Thus you might find A AND B written as ‘the intersection of A and B’ or ‘A intersection B’, or as A B (and said as “A cap B”), or as A • B .

An inclusive OR is indicated by (sometimes referred to as cup), written as ‘A B’ (and said as “A cup B”).

Another format you may come across is AND (A, B). Sometimes you will see a letter substituted for AND or other operators. For instance, function(A, B), or f(A, B). You will even see f replaced by a Greek or a German letter.

And on and on it goes ...

But always remember whatever words or signs are used, what matters is the definition set out in the truth table, and not the semantics and symbols/signs.

You can then build up compound formulae such as (~ A) B  but this format can be reduced to ~ A B. This is because, just like arithmetic connectives, an order of precedence is defined, where ~ (NOT) is more cohesive (applied first) than connectives like AND and OR, which are, in turn, more cohesive than [implies/implication, but remember the labels are not what matters, in this case‘implies’ has nothing to do with normal English meaning of the word ‘implication’] and [equivalence] [3].

Web abelard.org

bibliography

As a normal practice when I want a book in a subject, I go and sit for hours on the floor in a top-quality bookshop (and nowadays Amazon) and check, using the index of every book on the subject, to see how well all serious books cover several of the most difficult topics. The first two books in this list were obtained that way.

	Logic and Philosophy: A Modern Introduction by Paul Tidman, Howard Kahane £33.24 [amazon.co.uk] {advert} [amazon.com] Wadsworth Publishing Co Inc, hbk, 9th ed., 2001, 528 pages ISBN-10: 0534561721 ISBN-13: 978-0534561727 Note: there are several editions avaible, as well as paperback versions. However, because of the size of the book (528 pages), it is probably easier to handle with hard covers. This is the book that I would used as a background to teaching logic at any age, and will recommend for any intelligent adult wishing to pile in on their own.
	Introduction to Metamathematics by S.C. Kleene North Holland, hbk, 1980 (8th impression) ISBN-10: 0720421039 ISBN-13: 978-0720421033 £33.24 [amazon.co.uk] {advert} Ishi Press International, pbk, 2009 ISBN-10: 0923891579 ISBN-13: 978-0923891572 $29.95 [amazon.com] {advert} You want to take it higher? Then here is the best general book I know.
	Introduction to symbolic logic and its applications by Rudolf Carnap Dover Publications Inc., pbk, 1958 ISBN-10: 0486604535 ISBN-13: 978-0486604534 [amazon.com] [amazon.co.uk] I carried this with me everywhere I went for more than a decade. Make of that what you will.

end notes

1. Thus an individual item in the inner box may be said to be inside two boxes. The item remains in the inner box and, for clarity, this should not be forgotten. The nose of the horse is on the face of the horse, the horse is in the shop, the shop is in the town, the town is on the planet, etc. The horse’s nose is, therefore, on the planet. Because of the nature of reality, I assert that you may attend to only one of these relationships at any ‘one’ time.
   
   An objective of symbolic (set) logic is that you may substitute any assumption/axiom/property for the variables, and rely upon the result. This claim, in my view, is both dangerous and unsound to reality.
   
   In this situation, if ‘p’ (your apple) is contained in set A, and set A is contained in set B, then your apple is contained in set B - all very well if you are being crude and lacking in care. The universe of discourse, when the apple is said to be in set A, is not the same as the universe of discourse when the apple is said to be in set B. A new set has been added, for instance another basket.
   
   Consider you awake and put on your socks and shoes. You put your sock on your foot, and then place your shoe over the sock. Your foot is inside the sock, and the sock is inside the shoe, but your foot is not directly inside the shoe and your shoe is on the sock, not on your foot. Yes, you may say that your foot is in the shoe, but that is crude.
   
   Consider the plate is on the table. Is there a cloth on the table? Is the plate on the cloth, or is it on the table, or is it both? Again, it depends where is your focus. As a famous man [Bill Clinton] once said, it all depends on what ‘is’ is. Or, in these cases, what ‘on’ is, or , what ‘in’ is.
   
   Consider the house keys are in the house (set B). They are also in a kitchen drawer (set A). It will be a lot easier to find them if you know that they are in set A, as well as in set B.
   
   It is important that you discuss such examples with those learning logic, if they are not to become confused, or to believe that set logic is much more reliable and useful than is the reality.
   (With some assistance from James Hammerton in developing these examples.)
   
   
2. Logic or attribute blocks are available from several sources. A reliable source is from amazon.com or amazon.co.uk. An attribute blocks class set, also called a giant or jumbo set, similar to the set illustrated above, costs $25.95 [at amazon.com, as at 05/2013] or £30.99 [amazon.co.uk, as at 05/2013]. Its shipping weight is 6lb/4kg.
   
   
3. Two other truth tables of which you should be aware:

   truth table [implies]				truth table [equivalence]
   a	b	ab		a	b	ab
   True [T]	True [T]	True [T]		True [T]	True [T]	True [T]
   True [T]	False [F]	False [F]		True [T]	False [F]	False [F]
   False [F]	True [T]	True [T]		False [F]	True [T]	False [F]
   False [F]	False [F]	True [T]		False [F]	False [F]	True [T]

   
   

email email_abelard [at] abelard.org

© abelard, 2010, 15 january

all rights reserved

the web address for this page is https://www.abelard.org/sums/teaching_number_arithmetic_mathematics_understanding_sets.php

1640 words
prints as 7 A4 pages (on my printer and set-up)